题目内容
已知函数f(x)=4- (x>0),
(x>0),
(Ⅰ)求证:f(x)在(0,+∞)上是增函数;
(Ⅱ)若f(x)在[m,n]上的值域是[m,n](0<m<n),求m、n的值.
(Ⅰ)证明:设x1,x2∈(0,+∞),且x1<x2,
则
= .
.
∵x1,x2∈(0,+∞),且x1<x2,
∴x1-x2<0,x1x2>0,
则 <0.
<0.
即f(x1)<f(x2).
∴f(x)在(0,+∞)上是增函数;
(Ⅱ)∵f(x)在(0,+∞)上是增函数,
又f(x)在[m,n]上的值域是[m,n](0<m<n),
∴ ,
,
解得: .
.
∴ ,
, .
.
分析:(Ⅰ)直接利用函数单调性的定义证明;
(Ⅱ)根据(Ⅰ)中证出的函数在(0,+∞)上是增函数,结合f(x)在[m,n]上的值域是[m,n](0<m<n),列方程组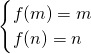 求解m和n的值.
求解m和n的值.
点评:本题考查了利用函数单调性的定义证明函数的单调性,在利用定义证明函数的单调性时,关键是作差判断符号,对于差式应化为最简形式,以免造成“证题用题”的现象,此题是基础题.
则

=
 .
.∵x1,x2∈(0,+∞),且x1<x2,
∴x1-x2<0,x1x2>0,
则
 <0.
<0.即f(x1)<f(x2).
∴f(x)在(0,+∞)上是增函数;
(Ⅱ)∵f(x)在(0,+∞)上是增函数,
又f(x)在[m,n]上的值域是[m,n](0<m<n),
∴
 ,
,解得:
 .
.∴
 ,
, .
.分析:(Ⅰ)直接利用函数单调性的定义证明;
(Ⅱ)根据(Ⅰ)中证出的函数在(0,+∞)上是增函数,结合f(x)在[m,n]上的值域是[m,n](0<m<n),列方程组
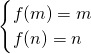 求解m和n的值.
求解m和n的值.点评:本题考查了利用函数单调性的定义证明函数的单调性,在利用定义证明函数的单调性时,关键是作差判断符号,对于差式应化为最简形式,以免造成“证题用题”的现象,此题是基础题.

练习册系列答案
相关题目