题目内容
已知等比数列{an}的前n项和为Sn,若S =4(a1+a3+a5+…+a2n-1),a1a2a3=27,则a6=( )
=4(a1+a3+a5+…+a2n-1),a1a2a3=27,则a6=( )
| A.27 | B.81 | C.243 | D.729 |
C
解析试题分析:∵ ,
, ,又∵
,又∵ ,∴
,∴ ,
,
∴ ,∴
,∴ ,故选C.
,故选C.
考点:1.等比数列的通项公式;2.等比数列前n项和.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在等比数列{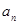 }中,
}中,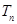 表示前n项的积,若T5=1,则( )
表示前n项的积,若T5=1,则( )
| A.a1=1 | B.a3=1 | C.a4=1 | D.a5=1 |
等比数列 中,
中, 前三项和为S3=27,则公比q的值是( )
前三项和为S3=27,则公比q的值是( )
| A.1 | B.- | C.1或- | D.-1或- |
已知等比数列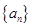 的前
的前 项和为
项和为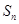 ,则下列一定成立的是( )
,则下列一定成立的是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 .则 .则 |
设等比数列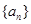 的公比为
的公比为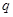 ,前
,前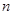 项和为
项和为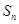 ,且
,且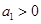 .若
.若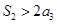 ,则
,则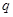 的取值范围是( )
的取值范围是( )
A.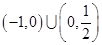 | B.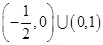 | C.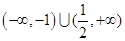 | D.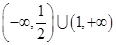 |
已知数列 是无穷等比数列,其前n项和是
是无穷等比数列,其前n项和是 ,若
,若 ,
, ,则
,则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
已知等比数列{an}的公比q为正数,且2a3+a4=a5,则q的值为( )
A. | B.2 | C. | D.3 |
在正项等比数列{an}中,a1,a19分别是方程x2-10x+16=0的两根,则a8·a10·a12等于( )
| A.16 | B.32 | C.64 | D.256 |
已知等比数列{an}满足an>0,n=1,2,…,且a5·a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n-1=( ).
| A.n(2n-1) | B.(n+1)2 | C.n2 | D.(n-1)2 |