已知函数f(x)=x|x-2|.＜3;在［0,a］上的最大值. 题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f(x)=x|x-2|.

(1)解不等式f(x)＜3;

(2)设0＜a＜2,求f(x)在［0,a］上的最大值.

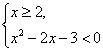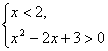
解:(1)∵x|x-2|＜3或2≤x＜3或x＜2,

∴不等式f(x)＜3的解集为{x|x＜3}.

(2)f(x)=x|x-2|=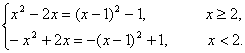

∴f(x)的单调递增区间是(-∞,1］和［2,+∞);单调递减区间是［1,2］.

①当0＜a≤1时,f(x)是［0,a］上的增函数,

此时f(x)在［0,a］上的最大值是f(a)=a(2-a);

②当1＜a＜2时,f(x)在［0,1］上是增函数,在［1,a］上是减函数,此时f(x)在［0,a］上的最大值是f(1)=1.

练习册系列答案

每日10分钟口算心算速算天天练系列答案

（2011•上海模拟）已知函数f(x)=(

-1)2+(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

4c2

k(k+c)

．

已知函数f(x)的图像在[a，b]上连续不断，f₁(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f₂(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f₂(x)－f₁(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x²，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．

已知函数f（x）、g（x），下列说法正确的是（）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

试题分类