题目内容
已知P是函数y=f(x)(x∈[m,n])图象上的任意一点,M、N为该图象的两个端点,点Q满足 =λ
=λ ,
, •i=0(其中0<λ<1,i为x轴上的单位向量),若|
•i=0(其中0<λ<1,i为x轴上的单位向量),若| |≤T(T为常数)在区间[m,n]上恒成立,则称y=f(x)在区间[m,n]上具有“T级线性逼近”.现有函数:①y=2x+1;②y=
|≤T(T为常数)在区间[m,n]上恒成立,则称y=f(x)在区间[m,n]上具有“T级线性逼近”.现有函数:①y=2x+1;②y= ;③y=x2.则在区间[1,2]上具有“
;③y=x2.则在区间[1,2]上具有“ 级 线性逼近”的函数的个数为( )
级 线性逼近”的函数的个数为( )A.0
B.1
C.2
D.3
【答案】分析:由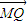 =λ
=λ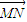 ,可得Q点在线段MN上,由
,可得Q点在线段MN上,由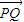 •
•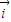 =0,可得P,Q两点的横坐标相等,故|
=0,可得P,Q两点的横坐标相等,故|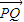 |即为P,Q两点纵坐标差的绝对值,分析三个函数中,x∈[1,2]时,|
|即为P,Q两点纵坐标差的绝对值,分析三个函数中,x∈[1,2]时,|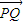 |≤
|≤ 是否恒成立,可得答案.
是否恒成立,可得答案.
解答:解:由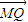 =λ
=λ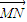 ,可得Q点在线段MN上,由
,可得Q点在线段MN上,由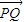 •
•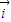 =0,可得P,Q两点的横坐标相等,故|
=0,可得P,Q两点的横坐标相等,故|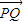 |即为P,Q两点纵坐标差的绝对值,
|即为P,Q两点纵坐标差的绝对值,
当f(x)=y=2x+1,x∈[1,2],则M(1,3),N(2,5),函数y=f(x)的图象即为线段MN,故|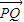 |=0≤
|=0≤ 恒成立,满足条件;
恒成立,满足条件;
当f(x)=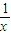 时,则M(1,1),N(2,
时,则M(1,1),N(2, ),线段MN的方程为y=-
),线段MN的方程为y=- x+
x+ ,此时|
,此时|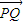 |=-
|=- x+
x+ -
-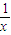 ,则|
,则|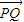 |′=-
|′=- +
+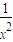 ,令|
,令|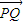 |′=0,则x=
|′=0,则x=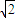 ,故当x=
,故当x=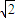 时,|
时,|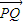 |取最大值
|取最大值 -
-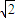 ,故|
,故|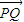 |≤
|≤ 恒成立,满足条件;
恒成立,满足条件;
当f(x)=x2.则M(1,1),N(2,4),线段MN的方程为y=3x-2,此时|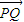 |=-x2+3x-2,当x=
|=-x2+3x-2,当x= 时,|
时,|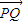 |取最大值
|取最大值 ,故|
,故|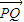 |≤
|≤ 恒成立,满足条件;
恒成立,满足条件;
故在区间[1,2]上具有“ 级线性逼近”的函数的个数为3个
级线性逼近”的函数的个数为3个
故选D
点评:本题考查的知识点函数恒成立问题,函数的值域,正确理解“T级线性逼近”定义,是解答的关键.
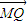 =λ
=λ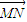 ,可得Q点在线段MN上,由
,可得Q点在线段MN上,由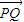 •
•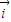 =0,可得P,Q两点的横坐标相等,故|
=0,可得P,Q两点的横坐标相等,故|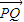 |即为P,Q两点纵坐标差的绝对值,分析三个函数中,x∈[1,2]时,|
|即为P,Q两点纵坐标差的绝对值,分析三个函数中,x∈[1,2]时,|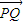 |≤
|≤ 是否恒成立,可得答案.
是否恒成立,可得答案.解答:解:由
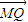 =λ
=λ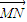 ,可得Q点在线段MN上,由
,可得Q点在线段MN上,由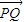 •
•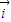 =0,可得P,Q两点的横坐标相等,故|
=0,可得P,Q两点的横坐标相等,故|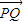 |即为P,Q两点纵坐标差的绝对值,
|即为P,Q两点纵坐标差的绝对值,当f(x)=y=2x+1,x∈[1,2],则M(1,3),N(2,5),函数y=f(x)的图象即为线段MN,故|
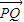 |=0≤
|=0≤ 恒成立,满足条件;
恒成立,满足条件;当f(x)=
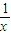 时,则M(1,1),N(2,
时,则M(1,1),N(2, ),线段MN的方程为y=-
),线段MN的方程为y=- x+
x+ ,此时|
,此时|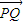 |=-
|=- x+
x+ -
-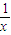 ,则|
,则|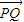 |′=-
|′=- +
+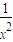 ,令|
,令|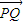 |′=0,则x=
|′=0,则x=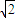 ,故当x=
,故当x=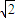 时,|
时,|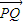 |取最大值
|取最大值 -
-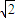 ,故|
,故|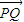 |≤
|≤ 恒成立,满足条件;
恒成立,满足条件;当f(x)=x2.则M(1,1),N(2,4),线段MN的方程为y=3x-2,此时|
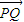 |=-x2+3x-2,当x=
|=-x2+3x-2,当x= 时,|
时,|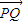 |取最大值
|取最大值 ,故|
,故|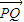 |≤
|≤ 恒成立,满足条件;
恒成立,满足条件;故在区间[1,2]上具有“
 级线性逼近”的函数的个数为3个
级线性逼近”的函数的个数为3个故选D
点评:本题考查的知识点函数恒成立问题,函数的值域,正确理解“T级线性逼近”定义,是解答的关键.

练习册系列答案
相关题目