题目内容
已知向量 ,
, ,设函数
,设函数 •
• ,若函数g(x)的图象与f(x)的图象关于坐标原点对称.
,若函数g(x)的图象与f(x)的图象关于坐标原点对称.(Ⅰ)求函数g(x)在区间[-
 ]上的最大值,并求出此时x的值;
]上的最大值,并求出此时x的值;(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若f(A)-g(A)=
 ,b+c=7,△ABC的面积为2
,b+c=7,△ABC的面积为2 ,求边a的长.
,求边a的长.
【答案】分析:(Ⅰ)利用向量的数量积公式,结合辅助角公式化简函数,再利用函数g(x)的图象与f(x)的图象关于坐标原点对称,确定g(x)的解析式,从而即可得到结论;
(Ⅱ)先求A,再利用△ABC的面积,求出bc,结合余弦定理,即可求边a的长.
解答:解:(Ⅰ)∵ ,
, ,
,
∴函数 =
= =
= -sin(2x+
-sin(2x+ ),
),
∵函数g(x)的图象与f(x)的图象关于坐标原点对称,
∴g(x)=- -sin(2x-
-sin(2x- ),
),
∵x∈[- ],∴2x-
],∴2x- ∈[-
∈[- ,
, ],
],
∴sin(2x- )∈[-1,
)∈[-1, ],
],
∴g(x)在区间[- ]上的最大值为
]上的最大值为 ,此时2x-
,此时2x- =-
=- ,即x=-
,即x=- ;
;
(Ⅱ)∵f(A)-g(A)= ,∴
,∴ -sin(2A+
-sin(2A+ ))+
))+ +sin(2A-
+sin(2A- )=
)= ,∴cos2A=-
,∴cos2A=- ,
,
∵A为锐角,∴A=
∵△ABC的面积为2 ,∴
,∴ ,∴bc=8
,∴bc=8
∵b+c=7,
∴ =(b+c)2-3bc=49-21=28
=(b+c)2-3bc=49-21=28
∴a=2 .
.
点评:本题考查向量知识的运用,考查三角函数的化简与三角函数的性质,考查余弦定理的运用,正确化简函数是关键.
(Ⅱ)先求A,再利用△ABC的面积,求出bc,结合余弦定理,即可求边a的长.
解答:解:(Ⅰ)∵
 ,
, ,
,∴函数
 =
= =
= -sin(2x+
-sin(2x+ ),
),∵函数g(x)的图象与f(x)的图象关于坐标原点对称,
∴g(x)=-
 -sin(2x-
-sin(2x- ),
),∵x∈[-
 ],∴2x-
],∴2x- ∈[-
∈[- ,
, ],
],∴sin(2x-
 )∈[-1,
)∈[-1, ],
],∴g(x)在区间[-
 ]上的最大值为
]上的最大值为 ,此时2x-
,此时2x- =-
=- ,即x=-
,即x=- ;
;(Ⅱ)∵f(A)-g(A)=
 ,∴
,∴ -sin(2A+
-sin(2A+ ))+
))+ +sin(2A-
+sin(2A- )=
)= ,∴cos2A=-
,∴cos2A=- ,
,∵A为锐角,∴A=

∵△ABC的面积为2
 ,∴
,∴ ,∴bc=8
,∴bc=8∵b+c=7,
∴
 =(b+c)2-3bc=49-21=28
=(b+c)2-3bc=49-21=28∴a=2
 .
.点评:本题考查向量知识的运用,考查三角函数的化简与三角函数的性质,考查余弦定理的运用,正确化简函数是关键.

练习册系列答案
相关题目
 ,
, ,设函数
,设函数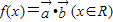 的图象关于直线
的图象关于直线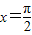 对称,其中ω为常数,且ω∈(0,1).
对称,其中ω为常数,且ω∈(0,1). ,再将所得图象向右平移
,再将所得图象向右平移 个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间
个单位,纵坐标不变,得到y=h(x)的图象,若关于x的方程h(x)+k=0在区间 上有且只有一个实数解,求实数k的取值范围.
上有且只有一个实数解,求实数k的取值范围. ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
, ,设函数
,设函数 ,x∈R.
,x∈R. ,求函数f(x)值域.
,求函数f(x)值域. ,
, ,设函数
,设函数 .
. 的最小正周期;
的最小正周期; 中,若
中,若 的面积为
的面积为 ,求实数
,求实数 的值.
的值.