题目内容
设椭圆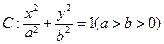 的一个顶点与抛物线
的一个顶点与抛物线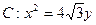 的焦点重合,
的焦点重合,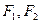 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率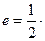 且过椭圆右焦点
且过椭圆右焦点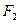 的直线
的直线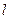 与椭圆C交于
与椭圆C交于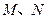 两点.
两点.
(1)求椭圆C的方程;
(2)是否存在直线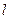 ,使得
,使得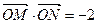 .若存在,求出直线
.若存在,求出直线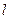 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(3)若AB是椭圆C经过原点O的弦, MN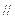 AB,求证:
AB,求证: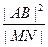 为定值.
为定值.
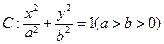 的一个顶点与抛物线
的一个顶点与抛物线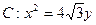 的焦点重合,
的焦点重合,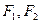 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率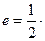 且过椭圆右焦点
且过椭圆右焦点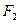 的直线
的直线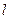 与椭圆C交于
与椭圆C交于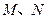 两点.
两点.(1)求椭圆C的方程;
(2)是否存在直线
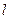 ,使得
,使得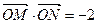 .若存在,求出直线
.若存在,求出直线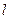 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.(3)若AB是椭圆C经过原点O的弦, MN
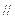 AB,求证:
AB,求证: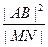 为定值.
为定值.(Ⅰ)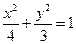 (Ⅱ)直线
(Ⅱ)直线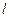 的方程为
的方程为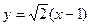 或
或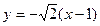 (III)略
(III)略
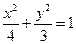 (Ⅱ)直线
(Ⅱ)直线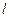 的方程为
的方程为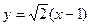 或
或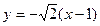 (III)略
(III)略(1) 椭圆的顶点为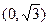 ,即
,即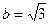 , 1分
, 1分
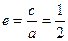 ,所以
,所以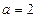 , 2分
, 2分
 椭圆的标准方程为
椭圆的标准方程为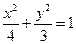 3分
3分
(2)由题可知,直线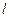 与椭圆必相交.
与椭圆必相交.
设存在直线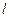 为
为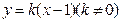 ,且
,且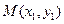 ,
,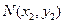 .
.
由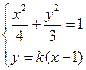 得
得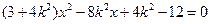 ,
,
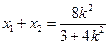 ,
,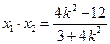 , 5分
, 5分
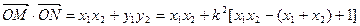
=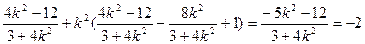 7分
7分
所以 ,故直线
,故直线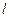 的方程为
的方程为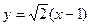 或
或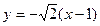 9分
9分
(3)设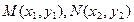 ,
,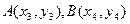
由(2)可得: |MN|=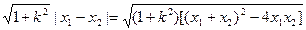
=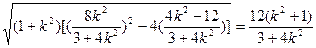 11分
11分
由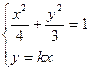 消去y,并整理得:
消去y,并整理得: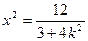 ,
,
|AB|=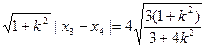 , 13分
, 13分
∴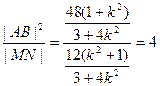 为定值 14分
为定值 14分
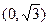 ,即
,即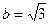 , 1分
, 1分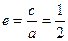 ,所以
,所以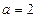 , 2分
, 2分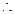 椭圆的标准方程为
椭圆的标准方程为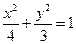 3分
3分 (2)由题可知,直线
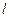 与椭圆必相交.
与椭圆必相交.设存在直线
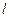 为
为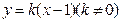 ,且
,且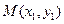 ,
,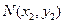 .
.由
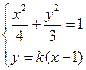 得
得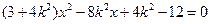 ,
, 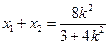 ,
,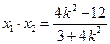 , 5分
, 5分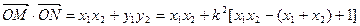
=
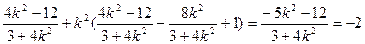 7分
7分 所以
 ,故直线
,故直线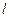 的方程为
的方程为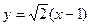 或
或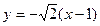 9分
9分(3)设
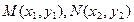 ,
,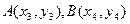
由(2)可得: |MN|=
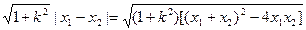
=
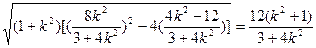 11分
11分由
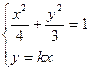 消去y,并整理得:
消去y,并整理得: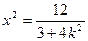 ,
,|AB|=
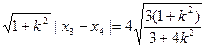 , 13分
, 13分∴
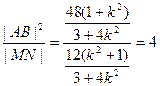 为定值 14分
为定值 14分
练习册系列答案
相关题目
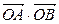 等于( )
等于( )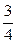
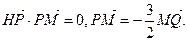
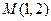 ,它们在
,它们在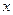 轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .
轴上有共同焦点,抛物线的顶点为坐标原点,则双曲线的标准方程是 .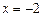 ,且直线l与x轴交于点M,圆
,且直线l与x轴交于点M,圆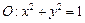 与x轴交于
与x轴交于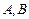 两点(如图).
两点(如图).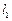 交圆于
交圆于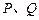 两点,且圆孤
两点,且圆孤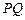 恰为圆周的
恰为圆周的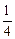 ,求直线
,求直线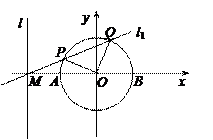
 交(II)中的一个椭圆于
交(II)中的一个椭圆于 两点,其中
两点,其中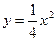 的焦点,离心率
的焦点,离心率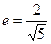 。(1)求椭圆的标准方程
。(1)求椭圆的标准方程 ;(2)过椭圆C的右焦点
;(2)过椭圆C的右焦点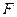 作直线
作直线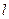 交椭圆C于A、B两点,交y轴于M,若
交椭圆C于A、B两点,交y轴于M,若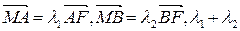 为定值吗?证明你的结论。
为定值吗?证明你的结论。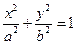 (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B,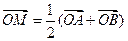 ,且
,且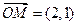 ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,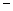 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率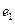 ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为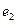 ,记
,记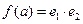 ,求
,求 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.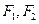 为椭圆
为椭圆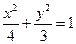 左、右焦点,过椭圆中心任作一条直线与椭圆交于
左、右焦点,过椭圆中心任作一条直线与椭圆交于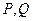 两点,当四边形
两点,当四边形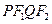 面积最大时,
面积最大时,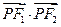 的值等于 .
的值等于 .