题目内容
(2014•广东模拟)设函数f(x)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b,(a,b∈R)
(1)求f(a)的值;
(2)若对任意的a∈[0,1],函数f(x)在x∈[0,1]上的最小值恒大于1,求b的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(1)求f(a)的值;
(2)若对任意的a∈[0,1],函数f(x)在x∈[0,1]上的最小值恒大于1,求b的取值范围.
分析:(1))由f(X)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b(a,b∈R),知f(a)=
a3-
(2a-1)a2+[a2-a-f(a)]a+b,由此能求出f(a).
=
.
(2)由f(X)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b(a,b∈R),知f′(x)=x2-(2a-1)x+a2-a-f′(a),由此能求出f′(a)=0.故f′(x)=x2-(2a-1)x+(a2-a)=[x-(a-1)](x-a),令f′(x)>0,得x<a-1,或x>a;令f′(x)<0,得a-1<x<a,故f(x)在(-∞,a-1]上单调递增,在[a-1,a]上单调递减,在[a,+∞)上单调递增,由此能求出b的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
=
| 2a3-3a2+6b |
| 6a+6 |
(2)由f(X)=
| 1 |
| 3 |
| 1 |
| 2 |
解答:解:(1)∵f(X)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b(a,b∈R)
∴f(a)=
a3-
(2a-1)a2+[a2-a-f(a)]a+b,
∴(a+1)f(a)=
a3-a3+
a2+a3-a2+b=
a3-
a2+b,
∴f(a)=
=
.
(2)∵f(X)=
x3-
(2a-1)x2+[a2-a-f(a)]x+b(a,b∈R)
∴f′(x)=x2-(2a-1)x+a2-a-f′(a),
∴f′(a)=a2-(2a-1)a+a2-a-f′(a),
∴f′(a)=0.
∴f′(x)=x2-(2a-1)x+(a2-a)=[x-(a-1)](x-a),
令f′(x)>0,得x<a-1,或x>a;令f′(x)<0,得a-1<x<a,
∴f(x)在(-∞,a-1]上单调递增,在[a-1,a]上单调递减,在[a,+∞)上单调递增,
∵0≤a≤1,∴f(x)在x∈[0,1]上的最小值为f(a)=
a3-
a2+b,
∴
a3-
a2+b>1在a∈[0,1]上恒成立.
即b>-
a3+
a2+1在a∈[0,1]上恒成立,
令g(x)=-
x2+
x2+1(0≤x≤1),
则g′(x)=-x2+x=-x(x-1)≥0,
∴g(x)在x∈[0,1]上单调递增,
∴1≤g(x)≤
,
∴b>
.
| 1 |
| 3 |
| 1 |
| 2 |
∴f(a)=
| 1 |
| 3 |
| 1 |
| 2 |
∴(a+1)f(a)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴f(a)=
| ||||
| a+1 |
| 2a3-3a2+6b |
| 6a+6 |
(2)∵f(X)=
| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2-(2a-1)x+a2-a-f′(a),
∴f′(a)=a2-(2a-1)a+a2-a-f′(a),
∴f′(a)=0.
∴f′(x)=x2-(2a-1)x+(a2-a)=[x-(a-1)](x-a),
令f′(x)>0,得x<a-1,或x>a;令f′(x)<0,得a-1<x<a,
∴f(x)在(-∞,a-1]上单调递增,在[a-1,a]上单调递减,在[a,+∞)上单调递增,
∵0≤a≤1,∴f(x)在x∈[0,1]上的最小值为f(a)=
| 1 |
| 3 |
| 1 |
| 2 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
即b>-
| 1 |
| 3 |
| 1 |
| 2 |
令g(x)=-
| 1 |
| 3 |
| 1 |
| 2 |
则g′(x)=-x2+x=-x(x-1)≥0,
∴g(x)在x∈[0,1]上单调递增,
∴1≤g(x)≤
| 7 |
| 6 |
∴b>
| 7 |
| 6 |
点评:本题考查利用导数求闭区间上函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
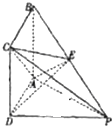 (2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
(2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.