题目内容
设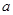 为实数,函数
为实数,函数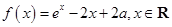 。
。
①求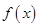 的单调区间与极值;
的单调区间与极值;
②求证:当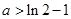 且
且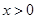 时,
时,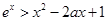 。
。
【答案】
(1)解:由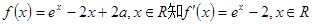
令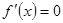 ,得
,得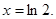 于是当
于是当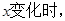
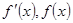 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
|
|
 故
故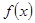 的单调递减区间是
的单调递减区间是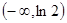 ,单调递增区间是
,单调递增区间是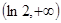 ,
,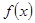 在
在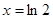 处取得极小值,极小值为
处取得极小值,极小值为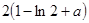
(2)设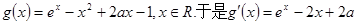 。对于任意的
。对于任意的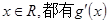 >0,所以
>0,所以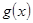 在R内单调递增。
在R内单调递增。
得到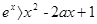 。
。
【解析】
试题分析:(1)解:由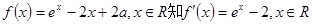
令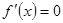 ,得
,得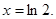 于是当
于是当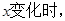
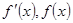 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
- |
0 |
+ |
|
|
|
|
|
故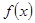 的单调递减区间是
的单调递减区间是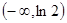 ,单调递增区间是
,单调递增区间是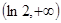 ,
,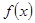 在
在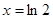 处取得极小值,极小值为
处取得极小值,极小值为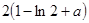
(2)证:设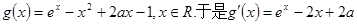 。由(1)知
。由(1)知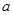 >
>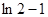 时,
时,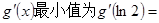
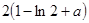 >0
>0
于是对于任意的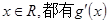 >0,所以
>0,所以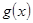 在R内单调递增。
在R内单调递增。
于是当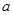 >
>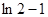 时,对任意的
时,对任意的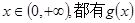 >
>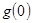
而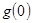 =0,从而对于任意的
=0,从而对于任意的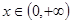 ,
,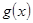 >0.
>0.
即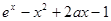 >0,故
>0,故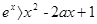
考点:本题主要考查导数计算,应用导数研究函数的单调性、极值,利用导数证明不等式。
点评:典型题,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值。不等式证明中,构造函数是关键。本题利用“本解法”,直观明了。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目





 为实数,函数
为实数,函数 。
。 ,求
,求 的最小值
的最小值  ,直接写出(不需要给出演算步骤)不等式
,直接写出(不需要给出演算步骤)不等式 的解集。
的解集。 为实数,函数
为实数,函数 。
。 的单调区间与极值;
的单调区间与极值; 且
且 时,
时, 。
。