题目内容
函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,A>0,ω>0)的部分图象如图所示,下列结论:
①最小正周期为π;
②将f(x)的图象向左平移![]() 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④![]() ;
;
⑤![]() .
.
其中正确的是( )

|
| A. | ①②③ | B. | ②③④ | C. | ①④⑤ | D. | ②③⑤ |
考点:
命题的真假判断与应用.
专题:
压轴题;三角函数的图像与性质.
分析:
根据已知中函数y=Asin(ωx+ϕ)(ω>0)的图象,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将(![]() ,﹣2)代入解析式,可求出ϕ值,进而求出函数的解析式,最后对照各选项进行判断即可.
,﹣2)代入解析式,可求出ϕ值,进而求出函数的解析式,最后对照各选项进行判断即可.
解答:
解:由图可得:函数函数y=Asin(ωx+ϕ)的最小值﹣|A|=﹣2,
令A>0,则A=2,又∵![]() =
=![]() ﹣
﹣![]() ,ω>0
,ω>0
∴T=π,ω=2,
∴y=2sin(2x+ϕ)
将(![]() ,﹣2)代入y=2sin(2x+ϕ)得sin(
,﹣2)代入y=2sin(2x+ϕ)得sin(![]() +ϕ)=﹣1
+ϕ)=﹣1
即![]() +ϕ=
+ϕ=![]() +2kπ,k∈Z
+2kπ,k∈Z
即ϕ=![]() +2kπ,k∈Z
+2kπ,k∈Z
∴f(x)=2sin(2x+![]() ).
).
∴f(0)=2sin![]() =
=![]() ,f(x+
,f(x+![]() )=2sin[2(x+
)=2sin[2(x+![]() )+
)+![]() ]=2sin(2x+
]=2sin(2x+![]() ).
).
f(![]() )=2sin(
)=2sin(![]() +
+![]() )=1.对称轴为直线x=
)=1.对称轴为直线x=![]() ,一个对称中心是(
,一个对称中心是(![]() ,0),故②③不正确;
,0),故②③不正确;
根据f(x)=2sin(2x+![]() )的图象可知,④
)的图象可知,④![]() 正确;
正确;
由于f(x)=2sin(2x+![]() )的图象关于点(
)的图象关于点(![]() ,0)中心对称,故⑤
,0)中心对称,故⑤![]() 正确.
正确.
综上所述,其中正确的是①④⑤.
故选C.
点评:
本题考查的知识点正弦型函数解析式的求法,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
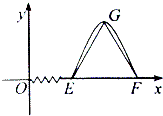 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2008)的值等于 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,