题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 在定义域上的单调性;
在定义域上的单调性;
(2)令函数![]() ,是自然对数的底数,若函数
,是自然对数的底数,若函数![]() 有且只有一个零点
有且只有一个零点![]() ,判断
,判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 或
或![]() 时,
时,![]() 在
在![]() 上单调递增, 当
上单调递增, 当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
(1)求出![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)根据函数的单调性求出
的减区间;(2)根据函数的单调性求出![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,由已知函数
,由已知函数![]() 有且仅有一个零点
有且仅有一个零点![]() ,则
,则![]() ,得
,得![]() ,令
,令![]() ,故
,故![]() ,利用导数研究函数的单调性,求出零点的分布情况,从而可求出
,利用导数研究函数的单调性,求出零点的分布情况,从而可求出![]() 的取值范围即可.
的取值范围即可.
(1)由已知![]() ,且
,且![]() ,
,
①当![]() 时,即当
时,即当![]() 时,
时,![]() ,
,
则函数![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,即
时,即![]() 或
或![]() 时,
时,![]() 有两个根,
有两个根,
![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
1°当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
2°当![]() 时,令
时,令![]() ,
,![]() ,
,
解得![]() ,
,
![]() 当
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增;
上单调递增;
3°当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减.
上单调递减.
(2)函数![]() ,
,
则![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调增,
上单调增,
当![]() ,所以
,所以![]()
所以![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,
,
当![]() ,所以
,所以![]() 为
为![]() 的最小值
的最小值
由已知函数![]() 有且只有一个零点
有且只有一个零点![]() ,则
,则![]()
所以![]() 则
则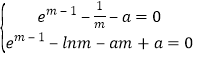
则![]() ,得
,得![]() ,
,
令![]() ,所以
,所以![]()
则![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减,
因为![]() ,
,
所以![]() 在
在![]() 上有一个零点,在
上有一个零点,在![]() 无零点,
无零点,
所以![]() .
.

【题目】某制造商3月生产了一批乒乓球,从中随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下:
分组 | 频数 | 频率 |
[39.95,39.97) | 10 | |
[39. 97,39.99) | 20 | |
[39.99,40.01) | 50 | |
[40.01,40.03] | 20 | |
合计 | 100 |

(Ⅰ)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图;
(Ⅱ)若以上述频率作为概率,已知标准乒乓球的直径为40.00 mm,试求这批球的直径误差不超过0.03 mm的概率;
(Ⅲ)统计方法中,同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).