Question

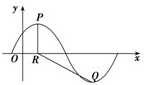已知函数f(x)=Asin (

π

3

x+φ)，x∈R，A＞0，0＜φ＜

π

2

．y=f（x）的部分图象，如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（1，A）．
（Ⅰ）求f（x）的最小正周期及φ的值；
（Ⅱ）若点R的坐标为（1，0），∠PRQ=

2π

3

，求A的值．

Answer 1

分析：（I）由已知函数f(x)=Asin (

π

3

x+φ)，我们易求出函数的最小正周期，又由P的坐标为（1，A），我们易构造出一个关于φ的三角方程，结合0＜φ＜

π

2

解三角方程即可求出φ值．
（II）根据（I）的结论及R的坐标，和∠PRQ=

2π

3

，利用余弦定理我们易构造出一个关于A的方程，解方程即可得到A的值．

解答：解：（I）由题意得，T=

2π

π 3

=6
∵P（1，A）在函数f(x)=Asin (

π

3

x+φ)的图象上
∴sin (

π

3

+φ)=1
又∵0＜φ＜

π

2

∴φ=

π

6

（II）由P、Q分别为该图象的最高点和最低点，点P的坐标为（1，A），结合（I）可知点Q的坐标为（4，-A）
连接PQ，在△PRQ中，∠PRQ=

2π

3

可得，∠QRX=

π

6

，作QM⊥X轴于M，则QM=A，RM=3，
所以有tan

π

6

=

3

3

=

QM

RM

=

A

3

∴A=

3

点评：本题考查的知识点是函数y=Asin（ωx+φ）的图象变换，三角函数的周期性及其求法，其中根据已知中条件构造关于参数A，φ是解答本题的关键．