题目内容
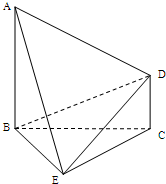 如图,已知AB⊥平面BCE,CD∥ab,△BCE是正三角形,AB=BC=2CD.
如图,已知AB⊥平面BCE,CD∥ab,△BCE是正三角形,AB=BC=2CD.(Ⅰ)在线段BE上是否存在一点F,使CF∥平面ADE?
(Ⅱ)求证:平面ADE⊥平面ABE;
(Ⅲ)求二面角A-DE-B的正切值.
分析:(I)取BE的中点F、AE的中点G,连接GD,GD,CF,由,△BCE是正三角形,AB=BC=2CD,结合三角形中位线性质,我们可得四边形CFGD是平行四边形,则CD∥GD,根据线面平行的判定定理,即可得到结论.
(II)由CF⊥BF,CF⊥AB,根据线面垂直判定定理可得CF⊥平面ABE,结合(I)中CF∥DG,可得DG⊥平面ABE,结合面面垂直的判定定理,可得平面ABE⊥平面ADE;
(III)过G作GM⊥DE,连接BM,我们可以得到∠BMG为二面角A-DE-B的平面角,解三角形BMG即可求出二面角A-DE-B的正切值.
(II)由CF⊥BF,CF⊥AB,根据线面垂直判定定理可得CF⊥平面ABE,结合(I)中CF∥DG,可得DG⊥平面ABE,结合面面垂直的判定定理,可得平面ABE⊥平面ADE;
(III)过G作GM⊥DE,连接BM,我们可以得到∠BMG为二面角A-DE-B的平面角,解三角形BMG即可求出二面角A-DE-B的正切值.
解答: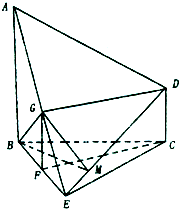 解:(Ⅰ)当F为BE的中点时,CF∥平面ADE…(1分)
解:(Ⅰ)当F为BE的中点时,CF∥平面ADE…(1分)
证明:取BE的中点F、AE的中点G,连接GD,GD,CF
∴GF=
AB,GF∥AB
又∵DC=
AB,CD∥AB
∴CD∥GF,CD=GF
∴CFGD是平行四边形…(3分)
∴CF∥GD
∴CF∥平面ADE…(4分)
(Ⅱ)∵CF⊥BF,CF⊥AB
∴CF⊥平面ABE
∵CF∥DG
∴DG⊥平面ABE…(6分)
∵DG?平面ABE
∴平面ABE⊥平面ADE…(7分)
(Ⅲ)∵AB=BE
∴AE⊥BG
∴BG⊥平面ADE
过G作GM⊥DE,连接BM,则BM⊥DE
则∠BMG为二面角A-DE-B的平面角…(9分)
设AB=BC=2CD=2,则
BG=
,GE=
在Rt△DCE中,CD=1,CE=2
∴DE=
又DG=CF=
由DE•GM=DG•EG得GM=
…(11分)
∴tan∠BMG=
=
∴面角A-DE-B的正切值
…(12分)
 解:(Ⅰ)当F为BE的中点时,CF∥平面ADE…(1分)
解:(Ⅰ)当F为BE的中点时,CF∥平面ADE…(1分)证明:取BE的中点F、AE的中点G,连接GD,GD,CF
∴GF=
| 1 |
| 2 |
又∵DC=
| 1 |
| 2 |
∴CD∥GF,CD=GF
∴CFGD是平行四边形…(3分)
∴CF∥GD
∴CF∥平面ADE…(4分)
(Ⅱ)∵CF⊥BF,CF⊥AB
∴CF⊥平面ABE
∵CF∥DG
∴DG⊥平面ABE…(6分)
∵DG?平面ABE
∴平面ABE⊥平面ADE…(7分)
(Ⅲ)∵AB=BE
∴AE⊥BG
∴BG⊥平面ADE
过G作GM⊥DE,连接BM,则BM⊥DE
则∠BMG为二面角A-DE-B的平面角…(9分)
设AB=BC=2CD=2,则
BG=
| 2 |
| 2 |
在Rt△DCE中,CD=1,CE=2
∴DE=
| 5 |
又DG=CF=
| 3 |
由DE•GM=DG•EG得GM=
| ||
| 5 |
∴tan∠BMG=
| BG |
| GM |
| ||
| 3 |
∴面角A-DE-B的正切值
| ||
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,二面角的平面角及求法,(I)、(II)的关键是熟练掌握直线与平面垂直及平行的判定定理、性质定理,(III)的关键是根据三垂线定理求出二面角的平面角.

练习册系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.