题目内容
如图,已知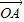 =
=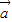 ,
,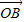 =
=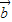 ,任意点M关于点A的对称点为S,点S关于点B的对称点为N.
,任意点M关于点A的对称点为S,点S关于点B的对称点为N.(1)用
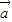 ,
,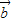 表示向量
表示向量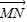 ;
;(2)设|
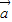 |=l,|
|=l,|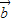 |=2,
|=2,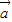 与
与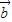 的夹角为30°,
的夹角为30°,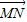 ⊥(λ
⊥(λ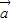 +
+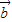 ),求实数λ的值.
),求实数λ的值.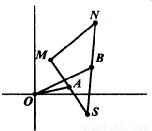
【答案】分析:(1)由题意可得,AB是△SMN的中位线,故有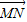 =2
=2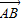 =2(
=2(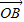 -
-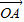 ),化简可得结果.
),化简可得结果.
(2)利用两个向量垂直的性质可得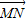 •(λ
•(λ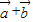 )=0,化简可得-λ
)=0,化简可得-λ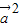 +
+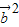 +(λ-1)
+(λ-1)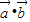 =0,由此求得实数λ的值.
=0,由此求得实数λ的值.
解答:解:(1)由题意可得,AB是△SMN的中位线,故有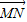 =2
=2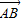 =2(
=2(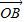 -
-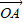 )=2(
)=2(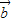 -
-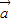 ).
).
(2)∵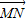 ⊥(λa+b),∴
⊥(λa+b),∴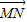 •(λ
•(λ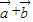 )=0,即 2(
)=0,即 2(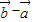 )•(λ
)•(λ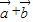 )=0,
)=0,
即-λ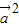 +
+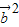 +(λ-1)
+(λ-1)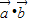 =0,
=0,
∴-λ+4+1×2×cos30°(λ-1)=0,
解得 λ=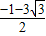 .
.
点评:本题主要考查两个向量的数量积的运算,向量在几何中的应用,两个向量垂直的性质,属于中档题.
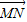 =2
=2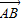 =2(
=2(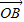 -
-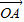 ),化简可得结果.
),化简可得结果.(2)利用两个向量垂直的性质可得
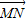 •(λ
•(λ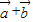 )=0,化简可得-λ
)=0,化简可得-λ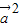 +
+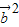 +(λ-1)
+(λ-1)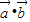 =0,由此求得实数λ的值.
=0,由此求得实数λ的值.解答:解:(1)由题意可得,AB是△SMN的中位线,故有
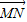 =2
=2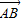 =2(
=2(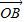 -
-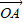 )=2(
)=2(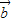 -
-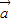 ).
).(2)∵
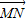 ⊥(λa+b),∴
⊥(λa+b),∴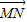 •(λ
•(λ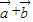 )=0,即 2(
)=0,即 2(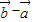 )•(λ
)•(λ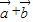 )=0,
)=0,即-λ
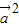 +
+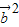 +(λ-1)
+(λ-1)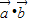 =0,
=0,∴-λ+4+1×2×cos30°(λ-1)=0,
解得 λ=
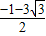 .
.点评:本题主要考查两个向量的数量积的运算,向量在几何中的应用,两个向量垂直的性质,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知函数f(x)=
,令g(x)=f(
).
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
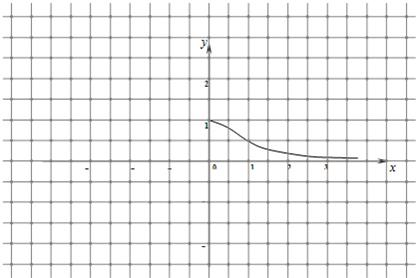
(3)如图,已知f(x)在区间[0,+∞)的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,并在同一坐标系中作出函数g(x)的图象.请说明你的作图依据.
| 1 |
| x2+1 |
| 1 |
| x |
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||||
f(x)-
|
… | |||||||
g(x)-
|
… |

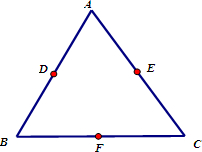 (2012•江苏一模)如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)
(2012•江苏一模)如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)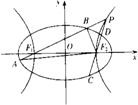 如图,已知椭圆
如图,已知椭圆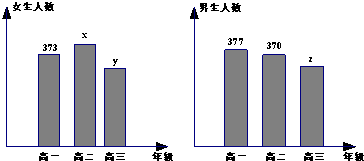 某学校共有高一、高二、高三学生2000名,各年级男、女生人数如图:已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
某学校共有高一、高二、高三学生2000名,各年级男、女生人数如图:已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19. (2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是
(2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是