题目内容
如图，正方形ABDE与等边△ABC所在平面互相垂直，AB=2，F为BD中点，G为CE中点．
（1）求证：FG∥平面ABC；
（2）求三棱锥F﹣AEC的体积．
（1）求证：FG∥平面ABC；
（2）求三棱锥F﹣AEC的体积．
（1）证：取AC中点H，连GH，BH
∵G为CE中点，
∴GH
又F为BD中点，ABDE为正方形，
∴BF
∴BFGH为平行四边形
∴FG∥BH
又BH
面ABC，
FG
面ABC
∴FG∥平面ABC
（2）解：∵面ABC⊥面ABDE于AB，EA⊥AB，EA
面ABDE
∴EA⊥面ABC，
∴GH⊥面ABC
∴GH⊥BH
又BH⊥AC，AC∩HG=H
∴BH⊥面AEC
∴FG⊥面ACE
∴
∵G为CE中点，
∴GH
又F为BD中点，ABDE为正方形，
∴BF
∴BFGH为平行四边形
∴FG∥BH
又BH
面ABC，FG
面ABC∴FG∥平面ABC
（2）解：∵面ABC⊥面ABDE于AB，EA⊥AB，EA
面ABDE∴EA⊥面ABC，
∴GH⊥面ABC
∴GH⊥BH
又BH⊥AC，AC∩HG=H
∴BH⊥面AEC
∴FG⊥面ACE
∴
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
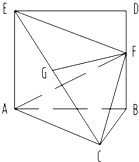（2011•武进区模拟）如图，正方形ABDE与等边△ABC所在平面互相垂直，AB=2，F为BD中点，G为CE中点．
如图，正方形ABDE与等边△ABC所在平面互相垂直，AB=2，F为BD中点，G为CE中点．
