题目内容
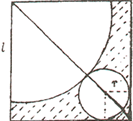 如图,将边长为5+
如图,将边长为5+| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:设圆锥底面圆的半径是r,母线为l,根据直线与圆相切、圆与圆相切的性质,结合正方形的边长为5+
得到l+(1+
)r=5
+2.再由扇形的弧长正好等于底面圆的周长,算出l=4r,从而解出r=
,进而可得此圆锥的体积.
| 2 |
| 2 |
| 2 |
| 2 |
解答:解:根据题意,欲在正方形内剪去阴影部分后裁剪出圆锥的底面,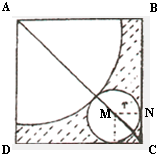
则圆锥的底面圆与正方形的边和以A为中心角的扇形的弧都相切,
设此时圆的圆心为M,与BC边相切于点N,设圆锥底面圆的半径是r,母线为l,
可得AC=AM+CM=5
+2,即l+(1+
)r=5
+2,
∵扇形的弧长正好等于底面圆的周长,即
πl=2πr,解之得l=4r,
∴两式联解可得r=
,
由此可得l=4
,圆锥的高h=
=
,
圆锥的体积V=
πr2h=
π×(
)2×
=
π.
故选:A

则圆锥的底面圆与正方形的边和以A为中心角的扇形的弧都相切,
设此时圆的圆心为M,与BC边相切于点N,设圆锥底面圆的半径是r,母线为l,
可得AC=AM+CM=5
| 2 |
| 2 |
| 2 |
∵扇形的弧长正好等于底面圆的周长,即
| 1 |
| 4 |
∴两式联解可得r=
| 2 |
由此可得l=4
| 2 |
| l2-r2 |
| 30 |
圆锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 30 |
2
| ||
| 3 |
故选:A
点评:本题将正方形裁剪出圆锥的平面展开图形,求该圆锥的体积.着重考查了正方形的性质、圆锥的侧面展开图、直线与圆相切的性质和圆与圆相切的性质等知识,属于中档题.

练习册系列答案
相关题目
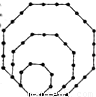
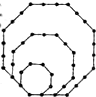 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是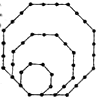 如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是________.
如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是________.