题目内容
函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时都有f(x1)≤f(x2),
则称函数f(x)在D上为非减函数,设f(x)在[0,1]上为非减函数,且满足以下条件:(1)
f(0)=0;(2)f(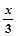 )=
)=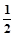 f(x);(3)f(1-x)=1-f(x),则f(
f(x);(3)f(1-x)=1-f(x),则f( )+f(
)+f(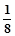 )=( )
)=( )
则称函数f(x)在D上为非减函数,设f(x)在[0,1]上为非减函数,且满足以下条件:(1)
f(0)=0;(2)f(
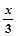 )=
)=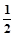 f(x);(3)f(1-x)=1-f(x),则f(
f(x);(3)f(1-x)=1-f(x),则f( )+f(
)+f(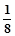 )=( )
)=( )A.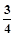 | B.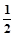 | C.1 | D.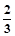 |
A
解:∵函数f(x)在[0,1]上为非减函数,①f(0)=0;③f(1-x)+f(x)=1,∴f(1)=1,
令x=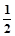 ,所以有f(
,所以有f(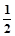 )=
)=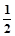 ,
,
又∵②f(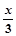 )=
)=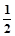 f(x),令x=1,有f(
f(x),令x=1,有f(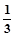 )=
)=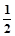 f(1)=
f(1)=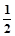 ,
,
令x=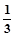 ,有f(
,有f( )=
)=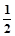 f(
f(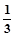 )=
)=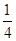 ,f(
,f(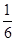 )=
)=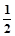 f(
f(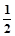 )=
)=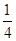 ,
,
非减函数性质:当x1<x2时,都有f(x1)≤f(x2),∴ <
<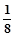 <
<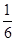 ,有f(
,有f( )≤f(
)≤f(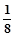 )≤f(
)≤f(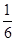 ),
),
而f( )=
)=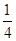 =f(
=f(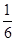 ),所以有 f(
),所以有 f(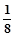 )=
)=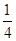 ,则 f(
,则 f(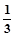 )+f(
)+f(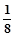 )=
)=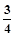 .
.
故答案为:A
令x=
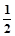 ,所以有f(
,所以有f(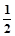 )=
)=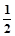 ,
,又∵②f(
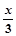 )=
)=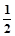 f(x),令x=1,有f(
f(x),令x=1,有f(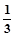 )=
)=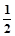 f(1)=
f(1)=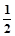 ,
,令x=
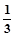 ,有f(
,有f( )=
)=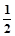 f(
f(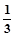 )=
)=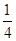 ,f(
,f(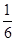 )=
)=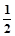 f(
f(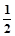 )=
)=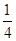 ,
,非减函数性质:当x1<x2时,都有f(x1)≤f(x2),∴
 <
<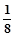 <
<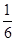 ,有f(
,有f( )≤f(
)≤f(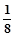 )≤f(
)≤f(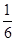 ),
),而f(
 )=
)=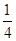 =f(
=f(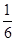 ),所以有 f(
),所以有 f(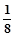 )=
)=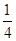 ,则 f(
,则 f(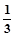 )+f(
)+f(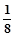 )=
)=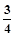 .
.故答案为:A

练习册系列答案
相关题目
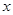 )=
)=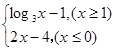 的反函数是
的反函数是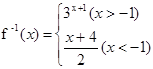

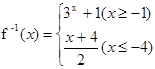
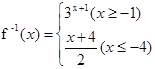
 的反函数为
的反函数为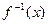 ,
,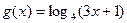 .
.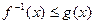 ,求
,求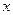 的取值范围D;
的取值范围D;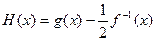 ,当
,当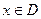 时,求函数
时,求函数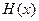 的值域.
的值域.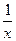 的图象上,点N与点M关于y轴对
的图象上,点N与点M关于y轴对 称且在直线x-y+3
称且在直线x-y+3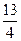 ,无最大值
,无最大值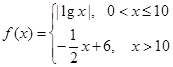 ,若
,若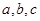 互不相等,且
互不相等,且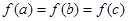 ,则
,则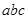 的取值范围是
的取值范围是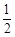 ,1)
,1)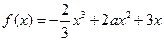 .
.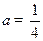 时,求函数
时,求函数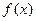 在
在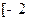 ,
,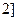 上的最大值、最小值;
上的最大值、最小值;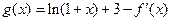 ,若
,若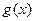 在
在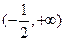 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.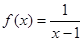 ,则函数
,则函数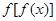 的定义域是( )
的定义域是( )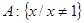
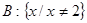
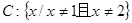

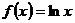 ,
,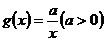 ,设
,设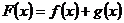 。
。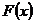 的单调区间;
的单调区间;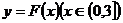 图像上任意一点
图像上任意一点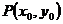 为切点的切线的斜率
为切点的切线的斜率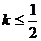 恒成立,求实数
恒成立,求实数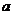 的最小值。
的最小值。