题目内容
已知数列{an}满足: ,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
(1)求数列{an},{bn}的通项公式
(2)证明:数列{bn}中的任意三项不可能成等差数列.
 ,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).
,anan+1<0(n≥1),数列{bn}满足:bn=an+12﹣an2(n≥1).(1)求数列{an},{bn}的通项公式
(2)证明:数列{bn}中的任意三项不可能成等差数列.
解:(1)由题意可知,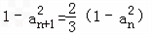
令cn=1﹣an2,则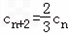
又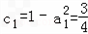 ,
,
则数列{cn}是首项为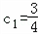 ,公比为
,公比为 的等比数列,
的等比数列,
即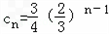 ,
,
故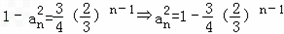 ,
,
又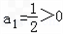 ,anan+1<0
,anan+1<0
故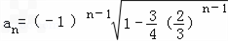
(2)假设数列{bn}存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,
由于数列{bn}是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
于是有2bs=br+bt成立,则只有可能有2br=bs+bt成立,
∴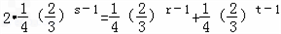 ,
,
由于r<s<t,所以上式左边为奇数,右边为偶数,故上式不可能成立,导致矛盾.
故数列{bn}中任意三项不可能成等差数列.
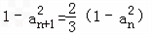
令cn=1﹣an2,则
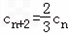
又
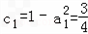 ,
,则数列{cn}是首项为
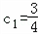 ,公比为
,公比为 的等比数列,
的等比数列,即
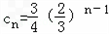 ,
,故
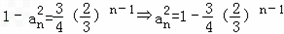 ,
,又
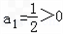 ,anan+1<0
,anan+1<0故
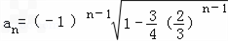
(2)假设数列{bn}存在三项br,bs,bt(r<s<t)按某种顺序成等差数列,
由于数列{bn}是首项为
 ,公比为
,公比为 的等比数列,
的等比数列,于是有2bs=br+bt成立,则只有可能有2br=bs+bt成立,
∴
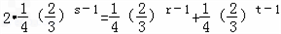 ,
,由于r<s<t,所以上式左边为奇数,右边为偶数,故上式不可能成立,导致矛盾.
故数列{bn}中任意三项不可能成等差数列.

练习册系列答案
相关题目