题目内容
已知两曲线参数方程分别为
(0≤θ<π)和
(t∈R),求它们的交点坐标.
|
|
分析:分别把参数方程化为普通方程,联立方程组求出它们的交点坐标.
解答:解:由
(0≤θ<π) 消去参数后的普通方程为
+y2=1(-
<x≤
,0≤y≤1),
由
(t∈R)消去参数后的普通方程为y2=
x,
联立两个曲线的普通方程得x=-5(舍)或x=1,
∴y=
,
所以它们的交点坐标为(1,
).
|
| x2 |
| 5 |
| 5 |
| 5 |
由
|
| 4 |
| 5 |
联立两个曲线的普通方程得x=-5(舍)或x=1,
∴y=
| 2 |
| 5 |
| 5 |
所以它们的交点坐标为(1,
| 2 |
| 5 |
| 5 |
点评:本题主要考查把参数方程化为普通方程的方法,求两曲线的交点坐标,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
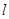 的参数方程为
的参数方程为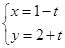 ,
曲线
,
曲线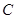 的极坐标方程为
的极坐标方程为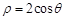 .
.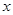 轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线
轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线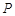 为直线
为直线 是曲线
是曲线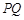 的最小值.
的最小值. 的参数方程为
的参数方程为 ,曲线
,曲线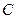 的极坐标方程为
的极坐标方程为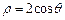 .
. 轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线
轴正半轴,建立直角坐标系,且在两种坐标系中取相同的长度单位,将曲线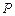 为直线
为直线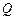 是曲线
是曲线 的最小值.
的最小值.