题目内容
一个暗箱里放着6个黑球、4个白球.(每个球的大小和质量均相同)不放回地依次取出2个球,若第1次取出的是白球,求第2次取到黑球的概率;有放回地依次取出2个球,求两球颜色不同的概率;有放回地依次取出3个球,求至少取到两个白球的概率.
分析:(1)不放回地依次取出2个球,若第1次取出的是白球,第二次取到黑球有6种可能,在第一次取到白球的情况下,第二次取球总可能数为9种;
(2)有放回地依次取出2个球,取球事件总数为10×10=100,两球颜色不同分为第一次取到黑球,第二次取到白求和第一次取到白求,第二次取到黑球,共2×6×4=48种;
(3)有放回地依次取出3个球,取球事件总数为10×10×10=1000,至少取到两个白球的事件包括两次取到白球,一次取到黑球及三次全是白球,共4×4×4+3×4×4×6=352种.
(2)有放回地依次取出2个球,取球事件总数为10×10=100,两球颜色不同分为第一次取到黑球,第二次取到白求和第一次取到白求,第二次取到黑球,共2×6×4=48种;
(3)有放回地依次取出3个球,取球事件总数为10×10×10=1000,至少取到两个白球的事件包括两次取到白球,一次取到黑球及三次全是白球,共4×4×4+3×4×4×6=352种.
解答:解:(1)设不放回地依次取出2个球,若第1次取出的是白球,第2次取到黑球的事件为A,则p(A)=
=
.
(2)设有放回地依次取出2个球,两球颜色不同的事件为B,则p(B)=
=
.
(3)设有放回地依次取出3个球,至少取到两个白球的时间为C,则p(C)=
=
.
| 6 |
| 9 |
| 2 |
| 3 |
(2)设有放回地依次取出2个球,两球颜色不同的事件为B,则p(B)=
| 48 |
| 100 |
| 12 |
| 25 |
(3)设有放回地依次取出3个球,至少取到两个白球的时间为C,则p(C)=
| 352 |
| 1000 |
| 44 |
| 125 |
点评:本题考查了古典概型中有放回和无放回问题,关键是要弄清有无放回的意义,正确把握各个事件的相互关系.

练习册系列答案
相关题目
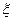 的分布列和期望.
的分布列和期望.