题目内容

有下列几个命题：

①有两个侧面都与底面垂直的棱柱是直棱柱；

②有两个对角面是矩形的棱柱是直棱柱；

③有一条侧棱垂直于底面两条边的棱柱是直棱柱；

④底面是正多边形的棱柱是正棱柱;

⑤高与侧棱、底面边长都相等的三棱柱是正棱柱.

其中正确命题的序号是________________.

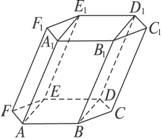
解析：如图所示，在斜六棱柱中，底面为正六边形，侧面AB1和侧面ED1都垂直于底面，则对角面AE1和对角面BD1都是矩形.在四棱柱ABDE—A1B1D1E1中，AA1⊥AE,且BB1⊥BD，故①②③④不正确.因为高与侧棱相等的棱柱为直棱柱,而底面为正多边形的直棱柱是正棱柱，所以⑤正确.故填⑤.

答案：⑤

小结：判断一个棱柱是否为直棱柱就是判断侧棱是否与底面垂直，侧棱与底面垂直的棱柱是直棱柱，侧棱与底面不垂直的棱柱不是直棱柱.一个棱柱满足它是直棱柱，底面又是正多边形时，这样的棱柱为正棱柱.

练习册系列答案
相关题目
有下列几个命题：
①函数y=2x2+x+1在（0，+∞）上不是增函数；②函数y=
1
x+1
在（-∞，-1）∪（-1，+∞）上是减函数；③函数y=
5+4x-x2
的单调区间是[-2，+∞）；④已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）．其中正确命题的序号是
 
．
13、下列几个命题中，
①有两个面互相平行，其余各面都是平行四边形的多面体是棱柱；
②有一个面是多边形，其余各面都是三角形的几何体叫棱锥；
③有两个面互相平行，其余各面都是等腰梯形的多面体是棱台；
④以直角三角形的一条直角边所在直线为轴旋转所得的旋转体是圆锥；
⑤以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台；
其中正确命题的序号是
④
．
有下列几个命题：①若
a
与
b
-
c
都是非零向量，则“
a
•
b
=
a
•
c
”是“
a
⊥(
b
-
c
)”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
15
7
；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
a
，
b
，
c
为同一平面内具有相同起点的任意三个非零向量，且满足
a
与
b
不共线，
a
⊥
c
，|
a
|=|
c
|，则|
b
•
c
|的值一定等于以
a
，
b
为邻边的平行四边形的面积．其中正确命题的序号是
 
．（写出全部正确结论的序号）
有下列几个命题：
①函数y=
1
x+1
在（-∞，-1）∪（-1，+∞）上是减函数；
②已知f（x）在R上是增函数，若a+b＞0，则有f（a）+f（b）＞f（-a）+f（-b）；
③已知函数y=f（x）是R上的奇函数，且当x≥0时，f(x)=x(1+
3x
)，则当x＜0时，f(x)=-x(1-
3x
)；
④已知定义在R上函数f（x）满足对?x，y∈R，f（x+y）=f（x）+f（y），且当x＞0时，f（x）＞0，则f（x）是R上的增函数；⑤如果a＞1，则函数f（x）=ax-x-a（a＞0且a≠1）有两个零点．
其中正确命题的序号是
 
．（写出全部正确结论的序号）
关于平面向量
a
，
b
，
c
，有下列几个命题：
①若
a
•
b
=
a
•
c
，则
a
=
0
或
b
=
c
；
②若
a
与
b
均为单位向量，它们的夹角为60°，则|
a
-3
b
|=
7
；
③若非零向量
a
，
b
，
c
满足|
a
|=|
b
|=|
c
|，
a
+
b
=
c
，则
a
与
b
的夹角为120°；
④若
a
=(1，-2)，
b
=(3，4)，则
a
在
b
方向上的投影是-1．
其中正确的是
②③④
②③④
．（请将所有正确命题的序号都填上）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网