题目内容
已知函数f（x）=asinx-bcosx（ab≠0）满足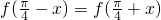
，则直线ax+by+c=0的斜率为________．
1
分析：依题意，f（x）的图象关于x=
对称，由f（0）=f（
）可求得a，b之间的关系，从而可求得答案．
解答：∵f（x）满足f（-x）=f（+x），
∴f（x）的图象关于x=对称，
∴f（0）=f（），
即-b=a，
∴直线ax+by+c=0的斜率k=-
=1．
故答案为：1．
点评：本题考查三角函数中的恒等变换应用，考查正弦函数的对称性，考查直线的斜率，属于中档题．
分析：依题意，f（x）的图象关于x=
对称，由f（0）=f（）可求得a，b之间的关系，从而可求得答案．解答：∵f（x）满足f（
-x）=f（+x），∴f（x）的图象关于x=
对称，∴f（0）=f（
），即-b=a，
∴直线ax+by+c=0的斜率k=-
=1．故答案为：1．
点评：本题考查三角函数中的恒等变换应用，考查正弦函数的对称性，考查直线的斜率，属于中档题．
练习册系列答案
相关题目