题目内容
若函数f(x)满足:对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,且f(x1)+f(x2)<f(x1+x2)成立,则称函数f(x)为“守法函数”.给出下列四个函数:①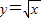 ;②y=log2(x+1);③y=2x-1;④y=cosx;其中“守法函数”的所有函数的序号是 .
;②y=log2(x+1);③y=2x-1;④y=cosx;其中“守法函数”的所有函数的序号是 .
【答案】分析:分别判断四个函数是否满足两个条件f(x1)>0,f(x2)>0和f(x1)+f(x2)<f(x1+x2)成立,然后确定“守法函数的序号”.
解答:解:①若f(x)=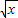 ,则对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,f(x1)+f(x2)=
,则对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,f(x1)+f(x2)=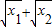 ,f(x1+x2)=
,f(x1+x2)=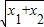 ,
,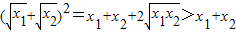 ,所以f(x1)+f(x2)>f(x1+x2),所以①不是“守法函数”.
,所以f(x1)+f(x2)>f(x1+x2),所以①不是“守法函数”.
②若f(x)=log2(x+1),对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,设x1=x2=1,则f(x1)+f(x2)=1+1=2,而f(x1+x2)=log23<2,所以f(x1)+f(x2)<f(x1+x2)不成立,所以②不是“守法函数”.
③若f(x)=2x-1,对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,f(x1)+f(x2)-f(x1+x2)=2x1-1+2x2-1-2x1+x2+1<0,则③是“守法函数”.④若f(x)=cosx,因为f(x)=cosx∈[-1,1],所以任意x1>0,x2>0,f(x1)>0,f(x2)>0不一定成立,所以④不是“守法函数”.
故答案为:③.
点评:本题考查了对数函数、三角函数、指数函数的单调性以及值域,运算量较大,综合性较强.
解答:解:①若f(x)=
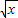 ,则对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,f(x1)+f(x2)=
,则对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,f(x1)+f(x2)=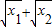 ,f(x1+x2)=
,f(x1+x2)=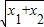 ,
,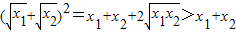 ,所以f(x1)+f(x2)>f(x1+x2),所以①不是“守法函数”.
,所以f(x1)+f(x2)>f(x1+x2),所以①不是“守法函数”.②若f(x)=log2(x+1),对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,设x1=x2=1,则f(x1)+f(x2)=1+1=2,而f(x1+x2)=log23<2,所以f(x1)+f(x2)<f(x1+x2)不成立,所以②不是“守法函数”.
③若f(x)=2x-1,对于任意x1>0,x2>0都有f(x1)>0,f(x2)>0,f(x1)+f(x2)-f(x1+x2)=2x1-1+2x2-1-2x1+x2+1<0,则③是“守法函数”.④若f(x)=cosx,因为f(x)=cosx∈[-1,1],所以任意x1>0,x2>0,f(x1)>0,f(x2)>0不一定成立,所以④不是“守法函数”.
故答案为:③.
点评:本题考查了对数函数、三角函数、指数函数的单调性以及值域,运算量较大,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目