题目内容
设z是虚数,满足ω=z+
是实数,且-1<ω<2.
(1)求|z|的值及z的实部的取值范围;
(2)设u=
.求证:u是纯虚数;
(3)求ω-u2的最小值.
| 1 |
| z |
(1)求|z|的值及z的实部的取值范围;
(2)设u=
| 1-z |
| 1+z |
(3)求ω-u2的最小值.
(1)由z是虚数,设z=a+bi(a,b∈R,b≠0)则ω=z+
=a+bi+
=a+bi+
=a+
+(b-
)i
∵ω∈R∴b-
=0且b≠0得a2+b2=1即|z|=1
此时,ω=2a,∵-1<ω<2∴-
<a<1即z的实部的取值范围为(-
,1).…(4分)
(2)u=
=
=
.
∵a2+b2=1
∴u=-
i又b≠0,-
<a<1故u是纯虚数.…(8分)
(3)ω-u2=2a+
=2a+
=2a+
=2[(a+1)+
]-3
由a∈(-
,1)知(a+1)+
≥2,
故当且仅当a+1=
,a=0时ω-u2的最小值为1.…(14分).
| 1 |
| z |
| 1 |
| a+bi |
| a-bi |
| a2+b2 |
| a |
| a2+b2 |
| b |
| a2+b2 |
∵ω∈R∴b-
| b |
| a2+b2 |
此时,ω=2a,∵-1<ω<2∴-
| 1 |
| 2 |
| 1 |
| 2 |
(2)u=
| 1-z |
| 1+z |
| 1-(a+bi) |
| 1+(a+bi) |
| [(1-a)-bi][(1+a)-bi] |
| (1+a)2+b2 |
∵a2+b2=1
∴u=-
| b |
| 1+a |
| 1 |
| 2 |
(3)ω-u2=2a+
| b2 |
| (1+a)2 |
| 1-a2 |
| (1+a)2 |
| 1-a |
| 1+a |
| 1 |
| a+1 |
由a∈(-
| 1 |
| 2 |
| 1 |
| a+1 |
故当且仅当a+1=
| 1 |
| a+1 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
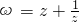 是实数,且-1<ω<2.
是实数,且-1<ω<2.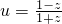 .求证:u是纯虚数;
.求证:u是纯虚数;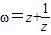 是实数,且-1<ω<2.
是实数,且-1<ω<2.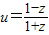 .求证:u是纯虚数;
.求证:u是纯虚数;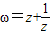 是实数,且-1<ω<2.
是实数,且-1<ω<2.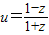 .求证:u是纯虚数;
.求证:u是纯虚数;