题目内容
（几何证明选讲选做题）如图，AB为⊙O的直径，C为⊙O上一点，AP和过C的切线互相垂直，垂足为P，过B的切线交过C的切线于T，PB交⊙O于Q，若∠BTC=120°，AB=4，则PQ•PB=3
3
．分析：连接AC、AB、OC，利用切线的性质定理可得：在四边形OBTC中，∠OCT=∠OBT=90°，从而得到∠COB=180°-120°=60°，故△OBC是等边三角形．接下来Rt△ABC中，利用三角函数定义得AC=ABsin60°=2
，再在Rt△PAC中，算出PC=ACcos60°=
，最后利用切割线定理得到PQ•PB=PC2=3．
| 3 |
| 3 |
解答：解：连接AC、AB、OC，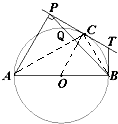
∵PT与圆O相切于点C，∴OC⊥PT，同理可得BT⊥AB
四边形OBTC中，∠OCT=∠OBT=90°
∴∠COB+∠CTB=180°，可得∠COB=180°-120°=60°
∵OC=OB，∴△OBC是等边三角形，可得∠OBC=60°
∵AB是圆O的直径，∴AC⊥BC，
Rt△ABC中，AB=4，可得AC=ABsin60°=2
∵PC与圆O相切于点C，∴∠PCA=∠CBA=60°
∵AP⊥PC，∴Rt△PAC中，PC=ACcos60°=
∵PC与圆O相切于点C，PQB是圆O的割线
∴PQ•PB=PC2=3
故答案为：3
∵PT与圆O相切于点C，∴OC⊥PT，同理可得BT⊥AB
四边形OBTC中，∠OCT=∠OBT=90°
∴∠COB+∠CTB=180°，可得∠COB=180°-120°=60°
∵OC=OB，∴△OBC是等边三角形，可得∠OBC=60°
∵AB是圆O的直径，∴AC⊥BC，
Rt△ABC中，AB=4，可得AC=ABsin60°=2
| 3 |
∵PC与圆O相切于点C，∴∠PCA=∠CBA=60°
∵AP⊥PC，∴Rt△PAC中，PC=ACcos60°=
| 3 |
∵PC与圆O相切于点C，PQB是圆O的割线
∴PQ•PB=PC2=3
故答案为：3
点评：本题借助于圆的切线和含有60°的直角三角形，求切线长的值，着重考查了直角三角形中三角函数的定义、四边形内角和与圆中的比例线段等知识，属于基础题．
练习册系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）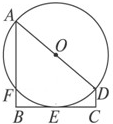
（几何证明选讲选做题）