题目内容
已知正项等差数列{an}的前n项和为Sn,其中a1≠a2,am、ak、ah都是数列{an}中满足ah-ak=ak-am的任意项.
(Ⅰ)证明:m+h=2k;
(Ⅱ)证明:Sm•Sh≤Sk2;
(III)若 也成等差数列,且a1=2,求数列
也成等差数列,且a1=2,求数列 的前n项和
的前n项和 .
.
解:(I)设数列{an}的公差为d,由题意a1<0,d>0.
∵ah-ak=ak-am,∴(h-k)d=(k-m)d,∴m+h=2k.…(2分)
(II)
 =
= ,∴Sm•Sh≤Sk2.…(6分)
,∴Sm•Sh≤Sk2.…(6分)
(III)取m=1,k=2,h=3,显然a1,a2,a3满足a3-a2=a2-a1.…(7分)
由 也成等差数列,则
也成等差数列,则 .
.
两边平方得 ,
,
再两边平方整理得4a12-4a1d+d2=0,即(2a1-d)2=0,
∴d=2a1=4.…(9分)
∴an=(2n-1)a,Sn=2n2,
∴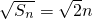 .,显然这时数列{an}满足题意. …(10分)
.,显然这时数列{an}满足题意. …(10分)
∴Sn-S1=2n2-2=2(n2-1).
∴ …(12分)
…(12分)
则 =
=
= .…(14分)
.…(14分)
分析:(I)根据等差数列的通项公式,用公差d,首项a1将ah,ak,am表示出,化简整理寻求h,k,m的关系.
(II)根据等差数列{an}的前n项和公式,将Sm•Sh与 Sk2 求出, ,Sk2=
,Sk2= 利用基本不等式,结合已知,
利用基本不等式,结合已知, ,(a1+am)(a1+ah)
,(a1+am)(a1+ah)  =(a1+ak)2合理的放缩转化,进行证明.
=(a1+ak)2合理的放缩转化,进行证明.
(III)不妨取m,n,h的一组特殊值寻求突破.取m=1,k=2,h=3.求得公差d,进而可求数列 的前n项和,再用放缩法可证.
的前n项和,再用放缩法可证.
点评:本题以数列为依托研究不等式问题,考查等差数列的性质、前n项公式及计算,放缩法证明不等式.要求有较强的分析解决问题的能力,具备特殊化法突破困难的意识.
∵ah-ak=ak-am,∴(h-k)d=(k-m)d,∴m+h=2k.…(2分)
(II)

 =
= ,∴Sm•Sh≤Sk2.…(6分)
,∴Sm•Sh≤Sk2.…(6分)(III)取m=1,k=2,h=3,显然a1,a2,a3满足a3-a2=a2-a1.…(7分)
由
 也成等差数列,则
也成等差数列,则 .
.两边平方得
 ,
,再两边平方整理得4a12-4a1d+d2=0,即(2a1-d)2=0,
∴d=2a1=4.…(9分)
∴an=(2n-1)a,Sn=2n2,
∴
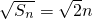 .,显然这时数列{an}满足题意. …(10分)
.,显然这时数列{an}满足题意. …(10分)∴Sn-S1=2n2-2=2(n2-1).
∴
 …(12分)
…(12分)则
 =
=
=
 .…(14分)
.…(14分)分析:(I)根据等差数列的通项公式,用公差d,首项a1将ah,ak,am表示出,化简整理寻求h,k,m的关系.
(II)根据等差数列{an}的前n项和公式,将Sm•Sh与 Sk2 求出,
 ,Sk2=
,Sk2= 利用基本不等式,结合已知,
利用基本不等式,结合已知, ,(a1+am)(a1+ah)
,(a1+am)(a1+ah)  =(a1+ak)2合理的放缩转化,进行证明.
=(a1+ak)2合理的放缩转化,进行证明.(III)不妨取m,n,h的一组特殊值寻求突破.取m=1,k=2,h=3.求得公差d,进而可求数列
 的前n项和,再用放缩法可证.
的前n项和,再用放缩法可证.点评:本题以数列为依托研究不等式问题,考查等差数列的性质、前n项公式及计算,放缩法证明不等式.要求有较强的分析解决问题的能力,具备特殊化法突破困难的意识.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
已知正项等差数列{an}的前20项和为100,则a5•a16的最大值是( )
| A、100 | B、75 | C、25 | D、50 |
已知正项等差数列{an}的前20项的和为100,那么a7a14的最大值为( )
| A、75 | B、100 | C、50 | D、25 |