题目内容
已知函数f(x)=2sin2x+sin2x,x∈[0,2π].求使f(x)为正值的x的集合.
解:法一:∵f(x)=1-cos2x+sin2x(2分)= (4分)
(4分)
∴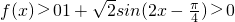
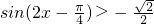 (6分)
(6分)
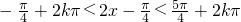 (8分)
(8分)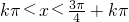 (10分)
(10分)
又x∈[0,2π].
∴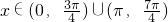 (12分)
(12分)
法二:f(x)=2sin2x+sin2x=2sin2x+2sinxcosx=2sinx(sinx+cosx)
f(x)为正值当且仅当sinx与sinx+cosx同号,
在x∈[0,2π]上,
若sinx与sinx+cosx均为正值,则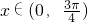 ;
;
若sinx与sinx+cosx均为负值,则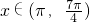
所以所求x的集合为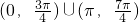 .
.
分析:法一:化简函数f(x)=2sin2x+sin2x,令其大于0,结合正弦函数的性质求出x的范围.
法二:可以对函数分解因式,分类讨论函数的正负,求出适合条件的x的范围即可.
点评:本题考查正弦函数的单调性,两角和与差的正弦函数,考查计算能力,是基础题.
 (4分)
(4分)∴
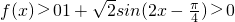
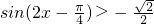 (6分)
(6分)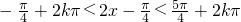 (8分)
(8分)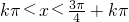 (10分)
(10分)又x∈[0,2π].
∴
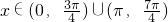 (12分)
(12分)法二:f(x)=2sin2x+sin2x=2sin2x+2sinxcosx=2sinx(sinx+cosx)
f(x)为正值当且仅当sinx与sinx+cosx同号,
在x∈[0,2π]上,
若sinx与sinx+cosx均为正值,则
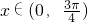 ;
;若sinx与sinx+cosx均为负值,则
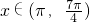
所以所求x的集合为
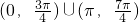 .
.分析:法一:化简函数f(x)=2sin2x+sin2x,令其大于0,结合正弦函数的性质求出x的范围.
法二:可以对函数分解因式,分类讨论函数的正负,求出适合条件的x的范围即可.
点评:本题考查正弦函数的单调性,两角和与差的正弦函数,考查计算能力,是基础题.

练习册系列答案
相关题目