题目内容
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为[0,1].
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
解析:
|
解:(1)∵f(x)=3x,∴f(a+2)=3a+2=18.∴3a=2. ∴g(x)=3ax-4x=(3a)x-4x. ∴g(x)=2x-4x. (2)令t=2x.∵x∈[0,1],且函数t=2x在区间[0,1]上单调递增,∴t∈[1,2]. 则y=t-t2=-(t2-t)=-(t ∵函数t=2x在区间[0,1]上单调递增,函数y=t-t2在[1,2]上单调递减, ∴函数g(x)的单调递减区间为[0,1]. 下面给出证明: 任取x1、x2∈[0,1],且x1<x2,则 g(x2)-g(x1)= = ∵0≤x1<x2≤1,∴ ∴2< ∴( ∴g(x2)<g(x1). ∴g(x1)>g(x2). ∴函数g(x)在区间[0,1]上单调递减. (3)∵g(x)在[0,1]上是减函数,∴g(1)≤g(x)≤g(0). ∴g(1)=21-41=-2,g(0)=20-40=0. ∴-2≤g(x)≤0. ∴函数g(x)的值域为[-2,0]. |
提示:
|
此题是一道有关函数的概念、函数性质及应用的推理、证明的综合题,做这类题目是可以从第(1)问寻找突破口,另外还要注意后面的各问分别以前面的(1)问作为提示或铺垫. (1)要求函数g(x)的解析式,关键是把式中a的值求出来,而这可以由已知条件f(a+2)=18解得,从而求出g(x)的解析式; (2)利用复合函数得单调性求g(x)的单调区间,并利用函数单调性得定义进行证明; (3)利用函数的单调性求函数g(x)在区间[0,1]上的值域. |

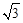 sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin ax cos ax+2 cos2 ax的周期为π,其中a>0. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. 的最大值;
的最大值; )>kg(x)对x∈[2,4]有解,求实数k的取值范围.
)>kg(x)对x∈[2,4]有解,求实数k的取值范围. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. ,无最小值
,无最小值