题目内容
已知集合A={x|0<ax+1≤5},集合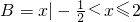 .
.
(1)若A⊆B,求实数a的取值范围;
(2)A,B能否相等?若能,求出a的值,若不能,试说明理由.
解:(1)若a=0,则A=R,不满足A⊆B;
若a>0,A={x|0<ax+1≤5}={x| },集合
},集合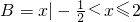 ,要使A⊆B,
,要使A⊆B,
则 ,解得:a≥2;
,解得:a≥2;
若a<0,A={x|0<ax+1≤5}={x| },集合
},集合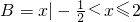 ,要使A⊆B,
,要使A⊆B,
则 ,解得:a<-8.
,解得:a<-8.
综上所述,使A⊆B的实数a的取值范围是(-∞,-8)∪[2,+∞).
(2)由(1)知,只有在a>0时A与B才有可能相等,由{x| }={x|
}={x| },得a=2,
},得a=2,
所以当a=2时,A,B相等.
分析:(1)题目给出的集合B是具体的,集合A含有字母a,所以需要对a的范围进行讨论,根据不同的情况,要使A⊆B,需根据两集合左右端点值的大小列式;
(2)由(1)知只有a>0时集合A和集合B有相等的可能,由它们的端点值相等就可以求a的值.
点评:本题考查了集合的包含关系的判断及应用,考查了分类讨论的数学思想,解答此题的关键是正确理解子集的概念.
若a>0,A={x|0<ax+1≤5}={x|
 },集合
},集合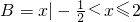 ,要使A⊆B,
,要使A⊆B,则
 ,解得:a≥2;
,解得:a≥2;若a<0,A={x|0<ax+1≤5}={x|
 },集合
},集合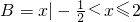 ,要使A⊆B,
,要使A⊆B,则
 ,解得:a<-8.
,解得:a<-8.综上所述,使A⊆B的实数a的取值范围是(-∞,-8)∪[2,+∞).
(2)由(1)知,只有在a>0时A与B才有可能相等,由{x|
 }={x|
}={x| },得a=2,
},得a=2,所以当a=2时,A,B相等.
分析:(1)题目给出的集合B是具体的,集合A含有字母a,所以需要对a的范围进行讨论,根据不同的情况,要使A⊆B,需根据两集合左右端点值的大小列式;
(2)由(1)知只有a>0时集合A和集合B有相等的可能,由它们的端点值相等就可以求a的值.
点评:本题考查了集合的包含关系的判断及应用,考查了分类讨论的数学思想,解答此题的关键是正确理解子集的概念.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
已知集合A={x|0≤2x-1≤3},集合B={x|x=sint},t∈R,则A∩B为( )
A、{x|
| ||
| B、{x|-1≤x≤1} | ||
C、{x|
| ||
D、{x|-
|