题目内容
(本小题满分12分)
 已知四棱锥
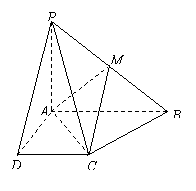
已知四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]() ,
,![]() ,
,![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求平面![]() 与平面APD所夹角的余弦值.
与平面APD所夹角的余弦值.
解:以A为坐标原点,AD.AB.AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则各点坐标为A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,![]() )
)
(1)因![]() =(1,1,0),
=(1,1,0),![]() =(0,2,-1),故|
=(0,2,-1),故|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,![]() =2,
=2,
所以![]() ,即
,即![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]()
(2)由![]() =(0,1,
=(0,1, ![]() ),
),![]() =(1,0,
=(1,0, ![]() ),,设平面AMC的法向量为
),,设平面AMC的法向量为![]() =(x,y,z),则
=(x,y,z),则![]() ·
·![]() =
=![]() ·
·![]() =0,解得
=0,解得![]() =(1,-1,2),
=(1,-1,2),
又平面PAD的法向量为![]() =(0,1,0),从而
=(0,1,0),从而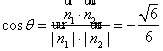
所以面AMC与面BMC夹角的余弦值为![]()

练习册系列答案
相关题目