题目内容
已知函数 的定义域为
的定义域为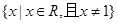 , 且
, 且 奇函数.当
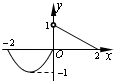
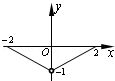
奇函数.当 时,
时,  =
= -
- -1,那么函数
-1,那么函数 ,当
,当 时,
时, 的递减区间是 ( )
的递减区间是 ( )
A. | B. | C. | D. |
C
解析试题分析:函数 是奇函数,说明
是奇函数,说明 的图象关于原点对称,而
的图象关于原点对称,而 的图象是由函数
的图象是由函数 的图象向左平移一个单位得到的,故反过来,把
的图象向左平移一个单位得到的,故反过来,把 的图象向右平移1个单位就得到函数
的图象向右平移1个单位就得到函数 的图象,因此函数
的图象,因此函数 的图象关于点
的图象关于点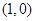 对称,那么函数
对称,那么函数 在关于点
在关于点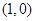 对称的区间上单调性相同(仿奇函数性质),而当
对称的区间上单调性相同(仿奇函数性质),而当 时,
时,  =
= -
- -1,其递减区间为
-1,其递减区间为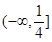 ,它关于点
,它关于点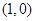 对称区间为
对称区间为 ,∴选C.
,∴选C.
考点:奇函数的性质及图象的平移.

练习册系列答案
相关题目
设 的定义域为
的定义域为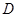 ,若
,若 满足下面两个条件,则称
满足下面两个条件,则称 为闭函数.
为闭函数.
① 在
在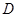 内是单调函数;②存在
内是单调函数;②存在 ,使
,使 在
在 上的值域为
上的值域为 ,
,
如果 为闭函数,那么
为闭函数,那么 的取值范围是( )
的取值范围是( )
A. ≤ ≤ | B. ≤ ≤ <1 <1 | C. | D. <1 <1 |
设 为定义在
为定义在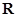 上的奇函数,当
上的奇函数,当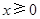 时,
时,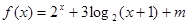 (
( 为常数),则
为常数),则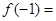 ( )
( )
A.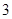 | B.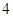 | C.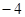 | D.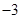 |
已知函数f(x)为奇函数,且当x>0时,f(x)=x2+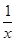 ,则f(-1)=( )
,则f(-1)=( )
| A.-2 | B.0 | C.1 | D.2 |
已知函数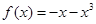 ,
,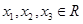 ,且
,且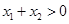 ,
,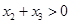 ,
,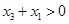 ,则
,则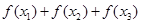 的值为
的值为
| A.正 | B.负 | C.零 | D.可正可负 |
已知偶函数 在
在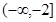 上是增函数,则下列关系式中成立的是( )
上是增函数,则下列关系式中成立的是( )
A.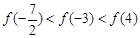 | B.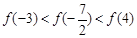 |
C.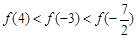 | D.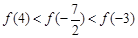 |
若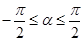 ,
,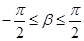 ,
,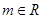 ,如果有
,如果有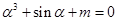 ,
,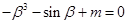 ,则
,则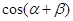 的值为( )
的值为( )
A.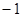 | B.0 | C.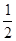 | D.1 |
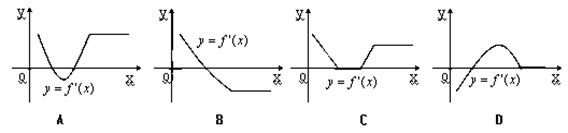
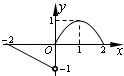
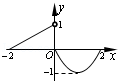
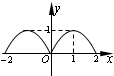
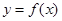 的图象如图所示,则导函数
的图象如图所示,则导函数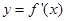 的图象的大致形状是( )
的图象的大致形状是( )