题目内容
设数集 ,且M、N都是集合
,且M、N都是集合 的子集,如果把
的子集,如果把 叫做集合
叫做集合 的“长度”,那么集合M∩N的“长度”的最小值是( )
的“长度”,那么集合M∩N的“长度”的最小值是( )
A. | B. | C. | D. |
C
解析试题分析:根据题意,M的长度为 ,N的长度为
,N的长度为 ,当集合M∩N的长度的最小值时,
,当集合M∩N的长度的最小值时,
M与N应分别在区间[0,1]的左右两端,故M∩N的长度的最小值是 +
+ -1=
-1= ,故选C.
,故选C.
考点:本试题主要考查了集合间的交集,应结合交集的意义,分析集合“长度”的定义,进而得到答案.
点评:解决该试题的关键是根据题意中集合“长度”的定义,可得M的长度为  ,N的长度为
,N的长度为  ,分析可得当集合M∩N的长度的最小值时,即重合部分最少时,M与N应分别在区间[0,1]的左右两端,进而计算可得答案.
,分析可得当集合M∩N的长度的最小值时,即重合部分最少时,M与N应分别在区间[0,1]的左右两端,进而计算可得答案.

练习册系列答案
相关题目
已知集合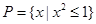 ,
,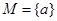 ,若
,若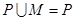 ,则a的取值范围是( )
,则a的取值范围是( )
A.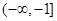 | B.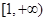 | C.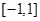 | D.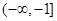 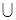 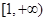 |
全集 ,集合
,集合 ,集合
,集合 ,则
,则
A. | B. | C. | D. |
已知集合A={a,2},集合B={a+1,5},若A∩B={2},则A∪B=
| A.{1,2} | B.{1,5} | C.{2,5} | D.{1,2,5} |
设集合 ,则
,则 ( )
( )
A. | B. |
C. | D. |
设不等式 的解集为
的解集为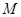 ,函数
,函数 的定义域为
的定义域为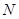 ,则
,则 为( )
为( )
A. | B. | C. | D. |
设集合 ,若集合
,若集合 ,则
,则 ( )
( )
A. | B. |
C. | D. |
定义集合 的一种运算:
的一种运算: ,若
,若 ,
, ,则
,则 中的所有元素之和为( )
中的所有元素之和为( )
| A.9 | B.14 | C.18 | D.21 |
设全集 ,
, ,
, ,则
,则
 (
( )等于( )
)等于( )
A. | B. | C. | D. |