题目内容
下列说法正确的是________(填上你认为正确的所有命题的序号)
①函数y=-sin(kπ+x)(k∈Z)是奇函数;
②函数y=2sin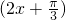 的图象关于点
的图象关于点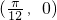 对称;
对称;
③函数y=2sin(2x+ )+sin(2x-
)+sin(2x- )的最小正周期是π;
)的最小正周期是π;
④△ABC中,cosA>cosB充要条件是A<B;
⑤函数y=cos2+sinx的最小值是-1.
①③④⑤
分析:根据函数y=Asin(ωx+∅)的图象特征,正弦函数的单调性、对称性,充分条件、必要条件、充要条件的定义,对各个选项进行判断,从而得出结论.
解答:由于①函数y=-sin(kπ+x)(k∈Z),即 y=±sinx,故函数是奇函数,故①正确.
②由于 函数y=2sin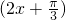 ,当x=
,当x= 时,函数y=2sin
时,函数y=2sin =2,为最大值,故y=2sin
=2,为最大值,故y=2sin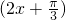 的图象关于直线x=
的图象关于直线x= 对称,故②不正确.
对称,故②不正确.
③由于 函数y=2sin(2x+ )+sin(2x-
)+sin(2x- )=3sin2xcos
)=3sin2xcos +cos2xsin
+cos2xsin =
= sin2x+
sin2x+ cos2x=
cos2x= sin(2x+
sin(2x+ ),其最小正周期等于
),其最小正周期等于 =π,故③正确.
=π,故③正确.
④△ABC中,由于函数 y=cosx 在(0,π)上是减函数,故cosA>cosB充要条件是 A<B,故④正确.
⑤函数y=cos2+sinx=1-sin2x+sinx=-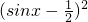 +
+ ,故当 sinx=-1 时,函数y=cos2+sinx 取得最小值-1,故⑤正确.
,故当 sinx=-1 时,函数y=cos2+sinx 取得最小值-1,故⑤正确.
故答案为 ①③④⑤.
点评:本题主要考查函数y=Asin(ωx+∅)的图象特征,正弦函数的单调性、对称性、周期性,充分条件、必要条件、充要条件的定义,属于中档题.
分析:根据函数y=Asin(ωx+∅)的图象特征,正弦函数的单调性、对称性,充分条件、必要条件、充要条件的定义,对各个选项进行判断,从而得出结论.
解答:由于①函数y=-sin(kπ+x)(k∈Z),即 y=±sinx,故函数是奇函数,故①正确.
②由于 函数y=2sin
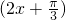 ,当x=
,当x= 时,函数y=2sin
时,函数y=2sin =2,为最大值,故y=2sin
=2,为最大值,故y=2sin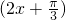 的图象关于直线x=
的图象关于直线x= 对称,故②不正确.
对称,故②不正确.③由于 函数y=2sin(2x+
 )+sin(2x-
)+sin(2x- )=3sin2xcos
)=3sin2xcos +cos2xsin
+cos2xsin =
= sin2x+
sin2x+ cos2x=
cos2x= sin(2x+
sin(2x+ ),其最小正周期等于
),其最小正周期等于 =π,故③正确.
=π,故③正确.④△ABC中,由于函数 y=cosx 在(0,π)上是减函数,故cosA>cosB充要条件是 A<B,故④正确.
⑤函数y=cos2+sinx=1-sin2x+sinx=-
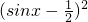 +
+ ,故当 sinx=-1 时,函数y=cos2+sinx 取得最小值-1,故⑤正确.
,故当 sinx=-1 时,函数y=cos2+sinx 取得最小值-1,故⑤正确.故答案为 ①③④⑤.
点评:本题主要考查函数y=Asin(ωx+∅)的图象特征,正弦函数的单调性、对称性、周期性,充分条件、必要条件、充要条件的定义,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目