题目内容
12.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinA-sinB=$\frac{1}{3}$sinC,3b=2a,2≤a2+ac≤18,设△ABC的面积为S,p=$\sqrt{2}$a-S,则p的最小值是( )| A. | $\frac{5\sqrt{2}}{9}$ | B. | $\frac{7\sqrt{2}}{9}$ | C. | $\sqrt{2}$ | D. | $\frac{9\sqrt{2}}{8}$ |
分析 由条件利用正弦定理求得c=a,b=$\frac{2a}{3}$,1≤a≤3,再利用余弦定理求得cosB的值,可得sinB 的值,从而△ABC的面积为S=$\frac{1}{2}$•ac•sinB 的值,可得p=$\sqrt{2}$a-$\frac{2\sqrt{2}}{9}$a2,再利用二次函数的性质求得p的最小值.
解答 解:在△ABC中,由sinA-sinB=$\frac{1}{3}$sinC利用正弦定理可得c=3a-3b,
再根据3b=2a,2≤a2+ac≤18,可得c=a,b=$\frac{2a}{3}$,1≤a≤3.
由余弦定理可得 b2=$\frac{{4a}^{2}}{9}$=a2+a2-2a•a•cosB,
求得cosB=$\frac{7}{9}$,∴sinB=$\frac{4\sqrt{2}}{9}$,∴△ABC的面积为S=$\frac{1}{2}$•ac•sinB=$\frac{{a}^{2}}{2}$•$\frac{4\sqrt{2}}{9}$=$\frac{2\sqrt{2}}{9}$•a2,
故p=$\sqrt{2}$a-S=$\sqrt{2}$a-$\frac{2\sqrt{2}}{9}$a2,再利用二次函数的性质结合a的范围可得当a=1时,p取得最小值是$\frac{7\sqrt{2}}{9}$,
故选:B.
点评 本题主要考查正弦定理和余弦定理的应用,属于基础题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
2.已知A(1,2,1),B(-1,3,4),C(1,1,1),$\overrightarrow{AP}$=2$\overrightarrow{PB}$,则$\overrightarrow{PC}$=( )
| A. | (-$\frac{1}{3}$,$\frac{8}{3}$,3) | B. | ($\frac{1}{3}$,-$\frac{8}{3}$,-3) | C. | (-$\frac{4}{3}$,$\frac{5}{3}$,2) | D. | ($\frac{4}{3}$,-$\frac{5}{3}$,-2) |
2.若椭圆经过原点,且焦点为F1(-1,0)、F2(-3,0),则其离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |

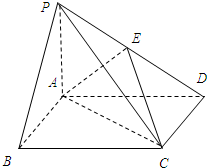 在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,
在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,