题目内容
设数列 的前
的前 项和为
项和为 ,满足
,满足 ,
, ,且
,且 .
.
(1)求 、
、 、
、 的值;
的值;
(2)求数列 的通项公式.
的通项公式.
(1) ,
, ,
, ;(2)
;(2) .
.
解析试题分析:(1)由 代入
代入 ,得到
,得到 ,然后由
,然后由 的值逐步算出
的值逐步算出 与
与 的值,然后利用
的值,然后利用 求出
求出 、
、 、
、 的值;(2)利用(1)中的结论归纳出
的值;(2)利用(1)中的结论归纳出 的通项公式,并以此归纳出
的通项公式,并以此归纳出 的表达式,然后利用数学归纳法证明数列
的表达式,然后利用数学归纳法证明数列 的通项公式的正确性.
的通项公式的正确性.
试题解析:(1)由 得
得 ,
,
整理得 ,因此有
,因此有 ,
,
即 ,解得
,解得 ,
,
同理有 ,即
,即 ,解得
,解得 ,
, ,
, ,
, ;
;
(2)由题意得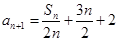 ,
,
由(1)知 ,
, ,
, ,猜想
,猜想 ,
,
假设当 时,猜想成立,即
时,猜想成立,即 ,则有
,则有 ,
,
则当 时,有
时,有 ,
,
这说明当 时,猜想也成立,
时,猜想也成立,
由归纳原理知,对任意 ,
, .
.
【考点定位】本题考查利用 与
与 的关系来考查数列的通项的求解,主要考查数学归纳法的应用,属于中等题.
的关系来考查数列的通项的求解,主要考查数学归纳法的应用,属于中等题.

练习册系列答案
相关题目
 ,把数列
,把数列 的各项排成如图所示的三角形数阵.记
的各项排成如图所示的三角形数阵.记 为该数阵的第
为该数阵的第 行中从左往右的第
行中从左往右的第 个数,则
个数,则 _______.
_______.
 中,
中,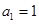 ,
, ,其通项公式
,其通项公式 = .
= .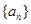 的前n项和
的前n项和 满足
满足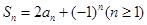
 、
、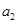 、
、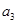 ;
;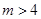 有
有
 =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. 的前
的前 项和为
项和为 满足
满足 ,且
,且 .
. 的值;
的值; ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数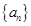 的前三项分别为
的前三项分别为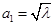 ,
, ,
,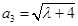 ,(其中
,(其中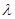 为正常数)。设
为正常数)。设
 。
。 的值;
的值;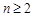 时,
时,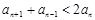 .
.