Question

【题目】抛物线的方程为，过抛物线上一点作斜率为的两条直线分别交抛物线于两点（三点互不相同），且满足：

（1）求抛物线的焦点坐标和准线方程；

（2）当时，若点的坐标为，求为钝角时点的纵坐标的取值范围；

（3）设直线上一点，满足，证明线段的中点在轴上；

Answer 1

【答案】（1）焦点，准线；（2）或；（3）证明见解析；

【解析】

（1）数形结合，依据抛物线C的标准方程写出焦点坐标和准线方程；

（2）为钝角时，必有,用表示，通过的范围可得的范围；

（3）先根据条件求出点M的横坐标，利用一元二次方程根与系数的关系，证明，可得的中点在轴上.

解：（1）由抛物线的方程为可得，焦点，准线；

（2）由点在上，可得，所以抛物线为，

设直线的直线方程，直线的直线方程,

点与是方程组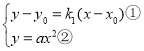的解，将②式代入①式得，

，可得 ③，可得

点与是方程组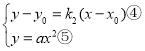的解，将⑤式代入⑤式得，

，可得 ，，

由已知得：，则 ⑥，

由③可得，代入，可得，

将代入⑥可得，代入，可得，

可得直线、分别与抛物线C得交点坐标为，

,于是,,

,

因为为钝角且三点互不相同，故必有，

可得得取值范围是，或，

又点得纵坐标满足，当，；

当时，，

故的取值范围：或；

（3）设点得坐标为,由，则，

将③与⑥式代入可得：，即，即线段的中点在轴上.