题目内容
选修4—5:不等式选讲
已知函数 ,
, .
.
(Ⅰ)当 时,求不等式
时,求不等式 的解集;
的解集;
(Ⅱ)设 ,且当
,且当 时,
时, ,求a的取值范围.
,求a的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)由 以及求不等式
以及求不等式 的解集,等价变换为
的解集,等价变换为 由分段函数即可到结论.
由分段函数即可到结论.
(Ⅱ)由 ,且当
,且当 即可化简函数
即可化简函数 ,由此可得
,由此可得 对
对 恒成立,所以x的最小值
恒成立,所以x的最小值 大于等于
大于等于 .即可得到结论.
.即可得到结论.
试题解析:(Ⅰ)当a=-2时,不等式 化为
化为 ,
,
设函数 ,则
,则

其图象如图所示

从图象可知,当且仅当 时,y<0,所以原不等式的解集是
时,y<0,所以原不等式的解集是 ;
;
(Ⅱ)当 ,
, ,不等式
,不等式 化为
化为 ,
,
所以 对
对 都成立,故
都成立,故 ,即
,即 ,
,
从而a的取值范围是 .
.
考点:1.绝对值.2.恒成立问题.
考点分析: 考点1:含绝对值的不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ”是“
”是“ ”的( )
”的( ) 向右平移
向右平移 个单位,得到函数
个单位,得到函数 的图象,则
的图象,则 ( )
( ) B.
B.  C.
C.  D.
D. 
 ,其中
,其中 表示不超过
表示不超过 的最大整数,如
的最大整数,如 ,
, ,
, ,若直线
,若直线
 与函数
与函数 的图象恰有两个不同的交点,则
的图象恰有两个不同的交点,则 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
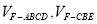 ,求
,求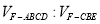 .
. ,若
,若 ,则a的取值范围是( )
,则a的取值范围是( ) B.
B. C.
C. D.
D.

 ( )
( ) B.
B. C.
C. D.
D.