题目内容
（2013•未央区三模）圆（x-4）2+y2=15与抛物线y2=4x的交点个数为
4
4
．分析：联立圆的方程和抛物线的方程，确定一元二次方程解的个数，即可得到结论．
解答：解：联立圆的方程和抛物线的方程：
，得x2-4x+1=0，
因为△=16-4=12＞0，所以圆（x-4）2+y2=15与抛物线y2=4x的交点个数为4．
故答案为：4
|
因为△=16-4=12＞0，所以圆（x-4）2+y2=15与抛物线y2=4x的交点个数为4．
故答案为：4
点评：本题考查圆与抛物线的位置关系，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
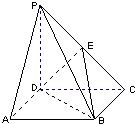（2013•未央区三模）如图，四棱锥P-ABCD的底面ABCD是正方形，棱PD⊥底面ABCD，PD=DC，E是PC的中点．
（2013•未央区三模）某三棱锥的三视图如图所示，该三棱锥的体积是为（ ）