题目内容
如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面.已知:直线a∥直线b,a⊥平面α,
求证:b⊥α.
证法一:如下图,在α内任取一条直线g.
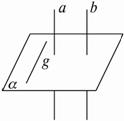
∵a⊥α,g![]() α,∴a⊥g.
α,∴a⊥g.
∵a∥b,∴b⊥g.
由直线和平面垂直的定义知b⊥α.
证法二:如下图设m、n是α内的两条相交直线.
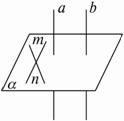
∵a⊥α,m、n![]() α,∴a⊥m,a⊥n.
α,∴a⊥m,a⊥n.
∵a∥b,∴b⊥m,b⊥n.
由直线和平面垂直的判定定理知b⊥α.
证法三:如下图,假设b和α不垂直,则在α内至少有一条直线c和b不垂直.
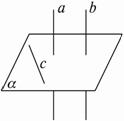
∵a⊥α,∴a⊥c.
∵a∥b,∴b⊥C.
这与b和C不垂直矛盾.
∴b⊥α.
点评:利用定义证明直线和平面垂直时,需在平面内任取一条直线;利用判定定理证明直线和平面垂直时,需在平面内取两条相交直线.证直线和平面垂直,最后都转化成了证直线和直线垂直.本例的结论也是判定直线和平面垂直的一种方法.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面. 上有无数个点不在平面
上有无数个点不在平面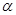 内,则
内,则