题目内容
已知抛物线y2=2px(p>0)的焦点为F,A,B,C为抛物线上三点.若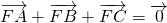 ,且
,且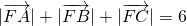 .
.
(1)求抛物线方程;
(2)(文)若OA⊥OB,直线AB与x轴交于一点(m,0),求m.
(2)(理)若以为AB为直径的圆经过坐标原点O,则求证直线AB经过一定点,并求出定点坐标.
解:(1)设A(x1,y1),B(x2,y2),C(x3,y3)
∵点A(x1,y1)在抛物线y2=2px上,
∴根据抛物线的定义得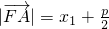 ,同理可得
,同理可得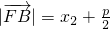 ,
,
∵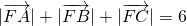 ,
,
∴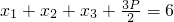 …①
…①
∵ ,∴
,∴ =(
=(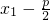 ,y1),
,y1), =(
=(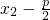 ,y2),
,y2),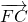 =(
=( ,y3),
,y3),
又∵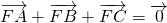 ,
,
∴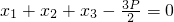 …②
…②
联解①②得:P=2
因此,抛物线方程为:y2=4x
(2)(文)设A(x1,y1),B(x2,y2),
∵OA⊥OB,∴ =x1x2+y1y2=0…③
=x1x2+y1y2=0…③
设过点m的直线方程为:y=k(x-m),
由 ,消去x得:ky2-4y-4km=0
,消去x得:ky2-4y-4km=0
由韦达定理得:y1y2=-4m,所以x1x2=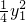 •
•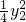 =
= (y1y2)2=m2,
(y1y2)2=m2,
将上式代入③,得m2+(-4m)=0,所以m=0(舍)或m=4.
(2)(理)设直线AB方程为:y-y1=k(x-x1),
其中斜率k= =
=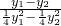 =
=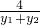
∴直线AB方程化为:y-y1=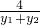 (x-x1),
(x-x1),
∵以为AB为直径的圆经过坐标原点O,
∴∠AOB=90°,可得向量 ,所以
,所以 =x1x2+y1y2=0…④
=x1x2+y1y2=0…④
∵A(x1,y1),B(x2,y2)都在抛物线y2=4x上,
∴x1= y12,x2=
y12,x2= y22,代入④得:
y22,代入④得: (y1y2)2+y1y2=0
(y1y2)2+y1y2=0
∴y1y2=-16(舍y1y2=0),可得y2=-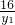 ,
,
将y2=-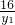 和
和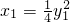 代入直线AB方程,化简可得:4x-(y1+
代入直线AB方程,化简可得:4x-(y1+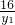 )y-16=0
)y-16=0
令y=0,得x=4,因此直线AB经过定点(4,0).
分析:(1)设A(x1,y1),B(x2,y2),C(x3,y3),根据根据抛物线的定义得: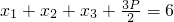 …①;根据向量的坐标运算得:
…①;根据向量的坐标运算得: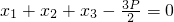 …②,联解①②可得抛物线方程为:y2=4x;
…②,联解①②可得抛物线方程为:y2=4x;
(2)(文)设A(x1,y1),B(x2,y2),根据OA⊥OB,得 =x1x2+y1y2=0…③.再由直线y=k(x-m)与抛物线方程消去x得:ky2-4y-4km=0,结合韦达定理得:y1y2=-4m,结合抛物线方程求得x1x2=
=x1x2+y1y2=0…③.再由直线y=k(x-m)与抛物线方程消去x得:ky2-4y-4km=0,结合韦达定理得:y1y2=-4m,结合抛物线方程求得x1x2= (y1y2)2=m2,将它代入③,得m2+(-4m)=0,所以m=0(舍)或m=4.
(y1y2)2=m2,将它代入③,得m2+(-4m)=0,所以m=0(舍)或m=4.
(理)设直线AB方程为:y-y1=k(x-x1),其中斜率k= =
=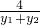 ,直线AB方程化为:y-y1=
,直线AB方程化为:y-y1=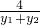 (x-x1).结合以为AB为直径的圆经过坐标原点O,
(x-x1).结合以为AB为直径的圆经过坐标原点O,
可以证明出x1x2+y1y2=0…④,将x1= y12,x2=
y12,x2= y22,代入④得:
y22,代入④得: (y1y2)2+y1y2=0,从而y1y2=-16,可得y2=-
(y1y2)2+y1y2=0,从而y1y2=-16,可得y2=-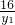 .最后将y2=-
.最后将y2=-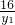 和
和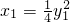 代入直线AB方程,化简可得:4x-(y1+
代入直线AB方程,化简可得:4x-(y1+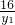 )y-16=0,再令y=0得x=4,因此直线AB经过定点(4,0).
)y-16=0,再令y=0得x=4,因此直线AB经过定点(4,0).
点评:本题以直线方程和向量的坐标运算为载体,着重考查了抛物线的标准方程和抛物线的简单几何性质,属于中档题.
∵点A(x1,y1)在抛物线y2=2px上,
∴根据抛物线的定义得
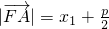 ,同理可得
,同理可得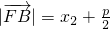 ,
,
∵
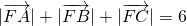 ,
,∴
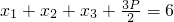 …①
…①∵
 ,∴
,∴ =(
=(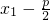 ,y1),
,y1), =(
=(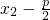 ,y2),
,y2),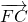 =(
=( ,y3),
,y3),又∵
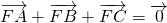 ,
,∴
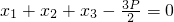 …②
…②联解①②得:P=2
因此,抛物线方程为:y2=4x
(2)(文)设A(x1,y1),B(x2,y2),
∵OA⊥OB,∴
 =x1x2+y1y2=0…③
=x1x2+y1y2=0…③设过点m的直线方程为:y=k(x-m),
由
 ,消去x得:ky2-4y-4km=0
,消去x得:ky2-4y-4km=0由韦达定理得:y1y2=-4m,所以x1x2=
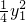 •
•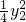 =
= (y1y2)2=m2,
(y1y2)2=m2,将上式代入③,得m2+(-4m)=0,所以m=0(舍)或m=4.
(2)(理)设直线AB方程为:y-y1=k(x-x1),
其中斜率k=
 =
=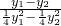 =
=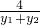
∴直线AB方程化为:y-y1=
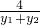 (x-x1),
(x-x1),∵以为AB为直径的圆经过坐标原点O,
∴∠AOB=90°,可得向量
 ,所以
,所以 =x1x2+y1y2=0…④
=x1x2+y1y2=0…④∵A(x1,y1),B(x2,y2)都在抛物线y2=4x上,
∴x1=
 y12,x2=
y12,x2= y22,代入④得:
y22,代入④得: (y1y2)2+y1y2=0
(y1y2)2+y1y2=0∴y1y2=-16(舍y1y2=0),可得y2=-
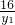 ,
,将y2=-
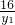 和
和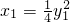 代入直线AB方程,化简可得:4x-(y1+
代入直线AB方程,化简可得:4x-(y1+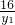 )y-16=0
)y-16=0令y=0,得x=4,因此直线AB经过定点(4,0).
分析:(1)设A(x1,y1),B(x2,y2),C(x3,y3),根据根据抛物线的定义得:
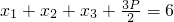 …①;根据向量的坐标运算得:
…①;根据向量的坐标运算得: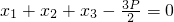 …②,联解①②可得抛物线方程为:y2=4x;
…②,联解①②可得抛物线方程为:y2=4x;(2)(文)设A(x1,y1),B(x2,y2),根据OA⊥OB,得
 =x1x2+y1y2=0…③.再由直线y=k(x-m)与抛物线方程消去x得:ky2-4y-4km=0,结合韦达定理得:y1y2=-4m,结合抛物线方程求得x1x2=
=x1x2+y1y2=0…③.再由直线y=k(x-m)与抛物线方程消去x得:ky2-4y-4km=0,结合韦达定理得:y1y2=-4m,结合抛物线方程求得x1x2= (y1y2)2=m2,将它代入③,得m2+(-4m)=0,所以m=0(舍)或m=4.
(y1y2)2=m2,将它代入③,得m2+(-4m)=0,所以m=0(舍)或m=4.(理)设直线AB方程为:y-y1=k(x-x1),其中斜率k=
 =
=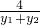 ,直线AB方程化为:y-y1=
,直线AB方程化为:y-y1=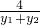 (x-x1).结合以为AB为直径的圆经过坐标原点O,
(x-x1).结合以为AB为直径的圆经过坐标原点O,可以证明出x1x2+y1y2=0…④,将x1=
 y12,x2=
y12,x2= y22,代入④得:
y22,代入④得: (y1y2)2+y1y2=0,从而y1y2=-16,可得y2=-
(y1y2)2+y1y2=0,从而y1y2=-16,可得y2=-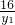 .最后将y2=-
.最后将y2=-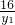 和
和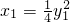 代入直线AB方程,化简可得:4x-(y1+
代入直线AB方程,化简可得:4x-(y1+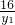 )y-16=0,再令y=0得x=4,因此直线AB经过定点(4,0).
)y-16=0,再令y=0得x=4,因此直线AB经过定点(4,0).点评:本题以直线方程和向量的坐标运算为载体,着重考查了抛物线的标准方程和抛物线的简单几何性质,属于中档题.

练习册系列答案
相关题目