题目内容
一质点沿直线运动，若由始点起经过t秒后的位移为s=
t3-
t2+2t+1，那么速度为0的时刻为（ ）
| 1 |
| 3 |
| 3 |
| 2 |
分析：位移对时间求导数即是速度，求出位移的导数，然后令其等于零解之即可求出所求．
解答：解：∵s=
t3-
t2+2t+1，，
∴v=s′（t）=t2-3t+2，
令v=0得，t2-3t+2=0，t1=1或t2=2．
故选D．
| 1 |
| 3 |
| 3 |
| 2 |
∴v=s′（t）=t2-3t+2，
令v=0得，t2-3t+2=0，t1=1或t2=2．
故选D．
点评：本题主要考查了导数的几何意义，导数的几何意义常在高考题的小题中或在大题的第一问中，属容易题．
练习册系列答案
相关题目
，那么速度为0的时刻为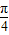
]，则点P到曲线y=f（x）对称轴距离的取值范围为[0，
]；
，那么速度为零的时刻只有1秒末；
内单调递增，则a的取值范围是
；
，那么速度为0的时刻为