题目内容
设f（x）=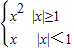
，g（x）是二次函数，若f（g（x））的值域是[0，+∞），则函数g（x）的值域是（ ）A．（-∞，-1]∪[1，+∞）
B．（-∞，-1]∪[0，+∞）
C．[0，+∞）
D．[1，+∞）
【答案】分析：先画出f（x）的图象，根据图象求出函数f（x）的值域，然后根据f（x）的范围求出x的范围，即为g（x）的取值范围，然后根据g（x）是二次函数可得结论．
解答：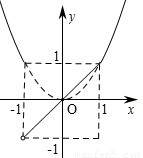
解：如图
为f（x）的图象，由图象知f（x）的值域为（-1，+∞），
若f（g（x））的值域是[0，+∞），只需g（x）∈（-∞，-1]∪[0，+∞）．
而g（x）是二次函数，故g（x）∈[0，+∞）．
故选：C
点评：本题主要考查了函数的图象，以及函数的值域等有关基础知识，同时考查了数形结合的数学思想，属于基础题．
解答：
解：如图为f（x）的图象，由图象知f（x）的值域为（-1，+∞），
若f（g（x））的值域是[0，+∞），只需g（x）∈（-∞，-1]∪[0，+∞）．
而g（x）是二次函数，故g（x）∈[0，+∞）．
故选：C
点评：本题主要考查了函数的图象，以及函数的值域等有关基础知识，同时考查了数形结合的数学思想，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目