题目内容
如图，已知圆中两条弦AB与CD相交于点F，CE与圆相切交AB延长线上于点E，若
，AF：FB：BE=4：2：1，则线段CE的长为________．
分析：设出AF=4k，BF=2k，BE=k，由DF•FC=AF•BF求出k的值，利用切割定理求出CE．
解答：由题意，设AF=4k，BF=2k，BE=k，由DF•FC=AF•BF，得8=8k2，∴k=1．
∴AF=4，BF=2，BE=1，
∴AE=7；
由切割线定理得CE2=BE•EA=1×7=7．
∴CE=
．故答案为：
点评：本题考查直线与圆的位置关系，考查计算能力，基本知识掌握的情况，是常考题型．
练习册系列答案
阅读快车系列答案
相关题目
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（2012•佛山二模）（几何证明选做题）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且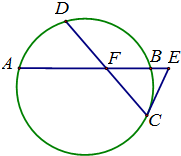
（2013•顺义区二模）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且
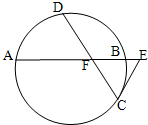（2012•石景山区一模）如图，已知圆中两条弦AB与CD相交于点F，CE与圆相切交AB延长线上于点E，若