题目内容
将函数y=cos(x- )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式是 ( )
个单位,则所得函数图象对应的解析式是 ( )
A.y=cos x x | B.y=cos(2x- ) ) |
C.y=sin(2x- ) ) | D.y=sin( x- x- ) ) |
D
解析试题分析:将函数y=cos(x- )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数y=cos(2x-
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数y=cos(2x- ),再向左平移
),再向左平移 个单位,得到函数图象的解析式为
个单位,得到函数图象的解析式为
y=cos(2x- )=cos[2(x+
)=cos[2(x+ )-
)- ]= y=sin(
]= y=sin( x-
x- ).
).
考点:本小题主要考查三角函数图象的平移变换,和诱导公式的应用,考查学生数形结合思想的应用.
点评:三角函数的图象平移变换要遵循左加右减的原则,而且平移的单位是针对而言的.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
若 则
则 的值是
的值是
A. | B. | C. | D. |
要得到函数 的图像, 需要将函数
的图像, 需要将函数 的图像( )
的图像( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
已知 是第四象限角,且
是第四象限角,且 ,则
,则 所在的象限是( )
所在的象限是( )
| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点 对称 对称 | B.偶函数且图像关于点 对称 对称 |
C.奇函数且图像关于直线 对称 对称 | D.偶函数且图像关于点 对称 对称 |
给定性质: ①最小正周期为π;②图象关于直线x=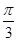 对称,则下列四个函数中,
对称,则下列四个函数中,
同时具有性质①、②的是( )
A.y = sin(2x- ) ) | B.y = sin( + + ) ) |
C.y = sin(2x+ ) ) | D.y = sin|x| |
 为锐角三角形,则
为锐角三角形,则

则 与
与 的大小关系为( )。
的大小关系为( )。
A. | B. | C. | D. |
sin(- π)的值等于( )
π)的值等于( )
A. | B.- | C. | D.- |
 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是