题目内容
下列结论正确的是
- A.?x∈R，使2x2-x+1＜0成立
- B.?x＞0，都有
成立 - C.函数
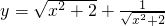的最小值为2 - D.0＜x≤2时，函数y=x-
有最大值为
D
分析：2x2-x+1=2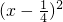
+
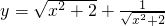＞0，x≤0时，B不成立，的最小值大于2，0＜x≤2时，函数D：y=x-有最大值为，成立．
解答：∵2x2-x+1=2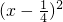+＞0，故A不成立；
当x≤0时，B不成立；
函数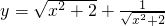的最小值大于2，故C不成立；
0＜x≤2时，函数y=x-有最大值为，D成立．
故选D．
点评：本题考查基本不等式的性质和应用，解题时要注意均值不等式的合理运用．
分析：2x2-x+1=2
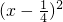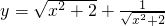+＞0，x≤0时，B不成立，的最小值大于2，0＜x≤2时，函数D：y=x-有最大值为，成立．解答：∵2x2-x+1=2
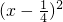+＞0，故A不成立；当x≤0时，B不成立；
函数
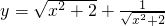的最小值大于2，故C不成立；0＜x≤2时，函数y=x-
有最大值为，D成立．故选D．
点评：本题考查基本不等式的性质和应用，解题时要注意均值不等式的合理运用．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
则下列结论正确的是( )
)=
B.P(ξ≥
)=
)=
D.P(ξ≤
)=P(ξ≥
)
且
则下列结论正确的是
B.
C. 
D. 
为“三件产品全不是次品”，
为“三件产品全是次品”，
为“三件产品不全是次品”，则下列结论正确的是:
：
，
，那么下列结论正确的是( )
，
B．
，
D．