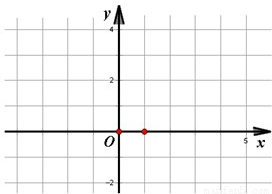
题目内容
设函数
(1)画出函数的图象;
(2)在x=0,x=3处函数f(x)是否连续;
(3)求函数f(x)的连续区间.
分析:本题考查函数f(x)在点x0处连续的定义及借助于图象的直观性分析、解决问题的能力.
解:(1)函数f(x)的图象如下:

(2)![]() f(x)=0,
f(x)=0,![]() f(x)=
f(x)=![]() x=0,
x=0,
∴![]() f(x)=0且f(0)=0.
f(x)=0且f(0)=0.
∴f(x)在点x=0处连续.
同理,f(x)在x=3处也连续.
(3)连续区间为(-∞,+∞).
点评:1.如何判断函数在点x0处的连续性呢?
(1)初等函数在定义域内都连续,因此其不连续点即函数无定义点;而连续函数极限符号“![]() ”与函数对应关系“f”可交换顺序,确定是否连续即可代入x0值,即
”与函数对应关系“f”可交换顺序,确定是否连续即可代入x0值,即![]() f(x)=f(x0).
f(x)=f(x0).
(2)考虑函数的连续性时还常常借助图象的直观性,即数形结合.
2.利用函数的连续性还可求参数的值或求函数在该点处的极限.

练习册系列答案
相关题目
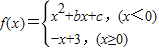 ,且f(-4)=f(0),f(-2)=-1.
,且f(-4)=f(0),f(-2)=-1.
 ,若f(-4)=f(0),f(-2)=-1,
,若f(-4)=f(0),f(-2)=-1,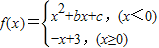 ,且f(-4)=f(0),f(-2)=-1.
,且f(-4)=f(0),f(-2)=-1.
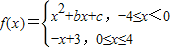 ,且f(-4)=f(0),f(-2)=-1.
,且f(-4)=f(0),f(-2)=-1.