题目内容
给出下列命题：
①若f'（x0）=0，则函数f（x）在x=x0处有极值；
②m＞0是方程
+
=1表示椭圆的充要条件；
③若f（x）=（x2-8）ex，则f（x）的单调递减区间为（-4，2）；
④A（1，1）是椭圆
+
=1内一定点，F是椭圆的右焦点，则椭圆上存在点P，使得PA+2PF的最小值为3．
其中为真命题的序号是______．
①若f'（x0）=0，则函数f（x）在x=x0处有极值；
②m＞0是方程
| x2 |
| m |
| y2 |
| 4 |
③若f（x）=（x2-8）ex，则f（x）的单调递减区间为（-4，2）；
④A（1，1）是椭圆
| x2 |
| 4 |
| y2 |
| 3 |
其中为真命题的序号是______．
若f'（x0）=0，函数f（x）在x=x0处可能取极值，但如果在x0两边单调性一致，则函数f（x）在x=x0处不取极值，故①错误；
m＞0且m≠0，是方程
+
=1表示椭圆的充要条件，故②错误；
若f（x）=（x2-8）ex，则f′（x）=（x2+2x-8）ex，当x∈（-4，2）时，f′（x）＜0，∴f（x）的单调递减区间为（-4，2），故③正确；
A（1，1）是椭圆
+
=1内一定点，F是椭圆的右焦点，则椭圆上存在点P（
，1），使得PA+2PF的最小值为3，故④正确；
故答案为：③④
m＞0且m≠0，是方程
| x2 |
| m |
| y2 |
| 4 |
若f（x）=（x2-8）ex，则f′（x）=（x2+2x-8）ex，当x∈（-4，2）时，f′（x）＜0，∴f（x）的单调递减区间为（-4，2），故③正确；
A（1，1）是椭圆
| x2 |
| 4 |
| y2 |
| 3 |
2
| ||
| 3 |
故答案为：③④
练习册系列答案
阅读快车系列答案
相关题目
＞0，则f(x)＞0；
dx＝4；
＝
．
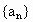成等比数列，
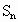是前n项和，则
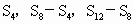成等比数列；
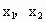，若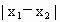
的最小值为π，则ω的值为2，θ的值为
；
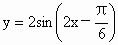的图象的一个对称点是
．