题目内容
要设计一个矩形,现只知道它的对角线长度为10,则在所有满足条件的设计中,面积最大的一个矩形的面积为
- A.50
- B.
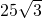
- C.

- D.100
A
分析:先设出矩形的长为a,宽为b,根据勾股定理可知a2+b2的值,进而根据基本不等式求得ab≤ (a2+b2)求得矩形面积的最大值.
(a2+b2)求得矩形面积的最大值.
解答:设矩形的长为a,宽为b,依题意可知a2+b2=100
∴矩形面积为:ab≤ (a2+b2)=50
(a2+b2)=50
故选A
点评:本题主要考查了基本不等式的应用.考查了学生运用所学知识解决实际问题的能力.
分析:先设出矩形的长为a,宽为b,根据勾股定理可知a2+b2的值,进而根据基本不等式求得ab≤
 (a2+b2)求得矩形面积的最大值.
(a2+b2)求得矩形面积的最大值.解答:设矩形的长为a,宽为b,依题意可知a2+b2=100
∴矩形面积为:ab≤
 (a2+b2)=50
(a2+b2)=50故选A
点评:本题主要考查了基本不等式的应用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
相关题目
要设计一个矩形,现只知道它的对角线长度为10,则在所有满足条件的设计中,面积最大的一个矩形的面积为( )
| A、50 | ||
B、25
| ||
C、50
| ||
| D、100 |

