题目内容
已知函数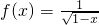 的定义域为M,函数g(x)=2x的值域为N,则M∩N=________.
的定义域为M,函数g(x)=2x的值域为N,则M∩N=________.
(0,1)
分析:先求出f(x)定义域M和g(x)的值域N,再进行交集运算.
解答:对于f(x),要满足1-x>0,即,x<1,故M={x|x<1}
对于g(x),由于g(x)=2x>0,故N={y|y>0}={x|x>0},
所以,M∩N={x|x<1}∩{x|x>0}=(0,1).
故答案为:(0,1).
点评:本题考查求函数的定义域和值域,求两个集合的交集的方法,化简M和N是解题的关键.
分析:先求出f(x)定义域M和g(x)的值域N,再进行交集运算.
解答:对于f(x),要满足1-x>0,即,x<1,故M={x|x<1}
对于g(x),由于g(x)=2x>0,故N={y|y>0}={x|x>0},
所以,M∩N={x|x<1}∩{x|x>0}=(0,1).
故答案为:(0,1).
点评:本题考查求函数的定义域和值域,求两个集合的交集的方法,化简M和N是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的定义域为M.
的定义域为M. 的定义域为M.
的定义域为M. 的定义域为M,函数
的定义域为M,函数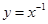 的定义域为N,则
的定义域为N,则 ( )
( ) 且
且 B.
B.  且
且 D.
D.

 的定义域为M,函数
的定义域为M,函数 的定义域为N,则
的定义域为N,则 的定义域为M,g(x)=
的定义域为M,g(x)= 的定义域为N,则M∩N=
的定义域为N,则M∩N= (B)
(B) (C)
(C) (D)
(D)