题目内容
(12分)在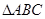 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是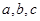 ,已知
,已知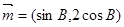 ,
,
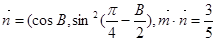 ,
,
(1)求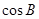 的值;
的值;
(2)若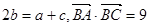 ,求
,求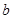 的值.
的值.
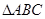 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是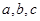 ,已知
,已知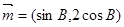 ,
,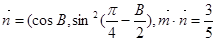 ,
,(1)求
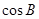 的值;
的值;(2)若
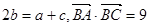 ,求
,求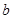 的值.
的值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)
 ,
, ,
, .
.(2)因为
 ,所以
,所以
 ,
,所以
 ,
,所以
 .
.点评:根据两个向量的数量积的坐标表示就是横坐标积与纵坐标积的和,得到关于B的方程,可求得cosB的值.第(2)问关键知道
 就是
就是 从而得到ac的值,再结合余弦定理的变形形式可得
从而得到ac的值,再结合余弦定理的变形形式可得 ,从而求出得b的值.
,从而求出得b的值.
练习册系列答案
相关题目
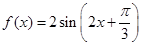
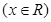
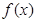 的最小正周期、单调增区间、对称轴和对称中心;
的最小正周期、单调增区间、对称轴和对称中心;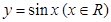 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?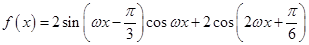 ,其中
,其中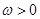 .
.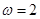 ,求函数f(x)的最小正周期;
,求函数f(x)的最小正周期;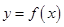 满足
满足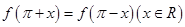 ,且
,且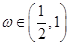 ,求函数f(x)的单调递减区间.
,求函数f(x)的单调递减区间.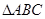 为锐角三角形,则
为锐角三角形,则

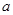 与
与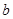 的大小关系为( )。
的大小关系为( )。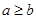



 ,则
,则 的值是( )
的值是( )



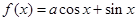 (
(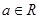 )在
)在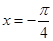 取到极值,
取到极值,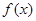 的解析式;
的解析式;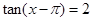 ,求
,求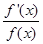 的值;
的值;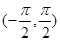 上的任取一个
上的任取一个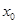 ,若
,若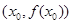 处的切线的斜率为
处的切线的斜率为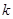 ,求
,求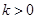 的概率.
的概率.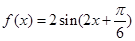 。
。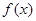 的振幅和最小正周期;
的振幅和最小正周期;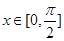 时,函数
时,函数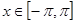 时,求
时,求 ,
, ,则
,则 的终边在( )
的终边在( )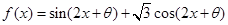 为奇函数,且在
为奇函数,且在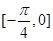 上为减函数的
上为减函数的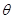 值可以是
值可以是