题目内容
(本题10分)
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人. 女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个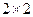 的列联表;
的列联表;
(Ⅱ)判断性别与休闲方式是否有关系.
解:(Ⅰ)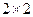 列联表为
列联表为
(Ⅱ)假设“休闲方式与性别无关”,计算得到 看电视 运动 合计 女 43 27 70 男 21 33 54 合计 64 60 124  的观察值
的观察值 .
.
因为 ,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有97.5%的把握认为休闲方式与性别有关.
,所以有理由认为假设“休闲方式与性别无关”是不合理的,即有97.5%的把握认为休闲方式与性别有关.
解析

 阅读快车系列答案
阅读快车系列答案(本小题满分12分)
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差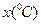 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数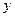 个 个 | 22 | 25 | 29 | 26 | 16 | 12 |
⑴求选取的2组数据恰好是相邻两个月的概率;
⑵若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出
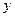 关于
关于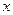 的线性回归方程
的线性回归方程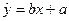 ;
;⑶若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性www.ks5u.com回归方程是否理想?
本小题满分12分)
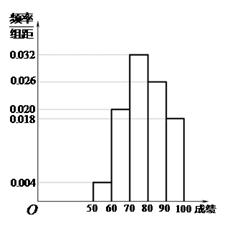
为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组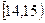 ……第五组
……第五组 ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.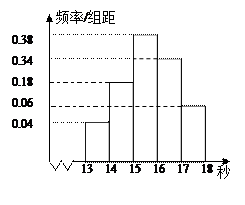
(Ⅰ)求这组数据的众数和中位数(精确到0.1);
(II)设 表示样本中两个学生的百米测
表示样本中两个学生的百米测
试成绩,已知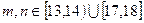
求事件“ ”的概率.
”的概率.
(Ⅲ) 根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如下 表
表
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | 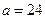 | 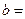 ______ ______ | _____ |
| 不达标 | 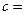 _____ _____ | 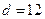 | _____ |
| 合计 | ______ | ______ | 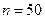 |
(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量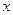 (吨)与相应的生产能耗
(吨)与相应的生产能耗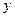 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
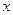 | 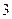 | 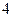 | 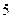 | 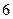 |
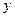 |  | 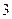 | 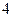 | 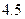 |
(2)请根据上表提供的数据,用最小二乘法求出
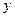 关于
关于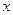 的线性回归方程
的线性回归方程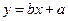 ;
;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
 (参考数值:
(参考数值: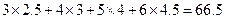 ,
,(
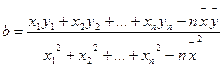 ,
,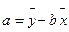 )
) (本小题满分12分)
下表是关于某设备的使用年限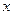 (年)和所需要的维修费用
(年)和所需要的维修费用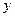 (万元)的几组统计数据:
(万元)的几组统计数据:
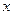 | 2 | 3 | 4 | 5 | 6 |
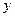 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(2)请根据上表提供的数据,用最小二乘法求出
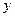 关于
关于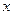 的线性回归方程
的线性回归方程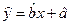 ;
;(3)估计使用年限为10年时,维修费用为 多少?
(参考数值:
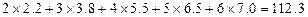 )
) (本题满分12分)班主任为了对本班学生的考试成绩进行分析,决定从全班 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为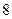 的样本进行分析。
的样本进行分析。
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本(只要求写出算式即可,不必计算出结果);
(Ⅱ)随机抽取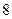 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: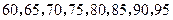 ;
;
物理成绩由低到高依次为: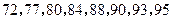 ,若规定
,若规定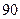 分(含
分(含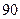 分)以
分)以 上为优秀,记
上为优秀,记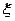 为这
为这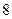 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求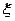 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)若这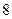 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:
| 学生编号 | 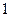 | 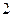 | 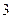 | 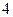 | 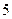 | 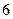 | 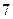 | 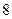 |
数学分数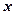 | 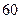 | 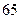 | 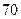 | 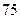 | 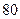 | 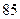 | 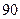 |  |
物理分数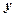 | 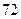 | 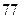 | 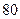 | 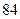 | 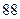 | 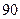 | 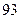 |  |
根据上表数据可知,变量
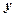 与
与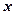
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出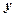 与
与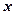 的线性回归方程(系数精确到
的线性回归方程(系数精确到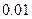 ).(参考公式:
).(参考公式: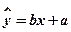 ,其中
,其中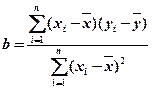 ,
,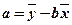 ; 参考数据:
; 参考数据: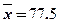 ,
,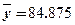 ,
,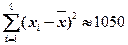 ,
, ,
,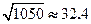 ,
,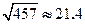 ,
,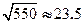 )
)  列联表;
列联表;